 por carvalhothg » Qui Set 22, 2011 15:24
por carvalhothg » Qui Set 22, 2011 15:24
Como calculo esta integral? Já tentei integração por partes e substituição de variável, mas não estou conseguindo. Alguém pode me dar uma ajuda?
-Calcule o valor de k ?? para que:
![\int_{-2}^{6}\left(x-k \right).\sqrt[3]{2+x}.dx=6 \int_{-2}^{6}\left(x-k \right).\sqrt[3]{2+x}.dx=6](/latexrender/pictures/f50b8b7fbe98f55122c52eecdee2789f.png)
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Neperiano » Qui Set 22, 2011 16:19
por Neperiano » Qui Set 22, 2011 16:19
Ola
Não tenho certeza, mas acho que você vai tenque passar o k pra frente da ingral, porque é uma constante
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Qui Set 22, 2011 18:04
por MarceloFantini » Qui Set 22, 2011 18:04
Note que
![\int_{-2}^6 (x-k) \sqrt[3]{2+x} \, \textrm{d}x = \int_{-2}^6 x \sqrt[3]{2+x} \, \textrm{d}x - \int_{-2}^6 k \sqrt[3]{2+x} \, \textrm{d}x \int_{-2}^6 (x-k) \sqrt[3]{2+x} \, \textrm{d}x = \int_{-2}^6 x \sqrt[3]{2+x} \, \textrm{d}x - \int_{-2}^6 k \sqrt[3]{2+x} \, \textrm{d}x](/latexrender/pictures/e7f09e3a32e0ab434eb311507306e474.png)
. Agora resolva as integrais usando k como constante e você encontrará seu valor.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qui Set 22, 2011 18:46
por LuizAquino » Qui Set 22, 2011 18:46
carvalhothg escreveu:Já tentei integração por partes e substituição de variável, mas não estou conseguindo.
Basta usar substituição de variáveis.
Fazendo u = 2 + x e du = dx, temos que:
![\int_{-2}^{6}\left(x-k \right)\sqrt[3]{2+x}\,dx \int_{-2}^{6}\left(x-k \right)\sqrt[3]{2+x}\,dx](/latexrender/pictures/d548bd2226f0c3bc244e13c9d776cbb1.png)
![= \int_{0}^{8}\left(u - 2 - k\right)\sqrt[3]{u}\,du = \int_{0}^{8}u^{\frac{4}{3}}\,du - (2+k)\int_{0}^{8}u^{\frac{1}{3}}\,du = \int_{0}^{8}\left(u - 2 - k\right)\sqrt[3]{u}\,du = \int_{0}^{8}u^{\frac{4}{3}}\,du - (2+k)\int_{0}^{8}u^{\frac{1}{3}}\,du](/latexrender/pictures/798764d656780fd7336cc78077184858.png)
Basta então calcular
k tal que:
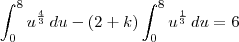
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por carvalhothg » Sex Set 23, 2011 19:18
por carvalhothg » Sex Set 23, 2011 19:18
Prof. Aquino,
porque você alterou os limites de integração? Como você encontrou 0 e 8?
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Neperiano » Sex Set 23, 2011 19:23
por Neperiano » Sex Set 23, 2011 19:23
Ola
Ele somou 2 nos dois limites de integração.
Não me lembro bem, mas acho que isto se deve ao fato do u = 2 + x
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Sex Set 23, 2011 19:27
por MarceloFantini » Sex Set 23, 2011 19:27
Sempre que fazemos uma mudança de variável em uma integral é necessário rever os limites de integração.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4611 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4579 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4342 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2843 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2865 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{-2}^{6}\left(x-k \right).\sqrt[3]{2+x}.dx=6 \int_{-2}^{6}\left(x-k \right).\sqrt[3]{2+x}.dx=6](/latexrender/pictures/f50b8b7fbe98f55122c52eecdee2789f.png)

![\int_{-2}^{6}\left(x-k \right).\sqrt[3]{2+x}.dx=6 \int_{-2}^{6}\left(x-k \right).\sqrt[3]{2+x}.dx=6](/latexrender/pictures/f50b8b7fbe98f55122c52eecdee2789f.png)


![\int_{-2}^6 (x-k) \sqrt[3]{2+x} \, \textrm{d}x = \int_{-2}^6 x \sqrt[3]{2+x} \, \textrm{d}x - \int_{-2}^6 k \sqrt[3]{2+x} \, \textrm{d}x \int_{-2}^6 (x-k) \sqrt[3]{2+x} \, \textrm{d}x = \int_{-2}^6 x \sqrt[3]{2+x} \, \textrm{d}x - \int_{-2}^6 k \sqrt[3]{2+x} \, \textrm{d}x](/latexrender/pictures/e7f09e3a32e0ab434eb311507306e474.png) . Agora resolva as integrais usando k como constante e você encontrará seu valor.
. Agora resolva as integrais usando k como constante e você encontrará seu valor.

![\int_{-2}^{6}\left(x-k \right)\sqrt[3]{2+x}\,dx \int_{-2}^{6}\left(x-k \right)\sqrt[3]{2+x}\,dx](/latexrender/pictures/d548bd2226f0c3bc244e13c9d776cbb1.png)
![= \int_{0}^{8}\left(u - 2 - k\right)\sqrt[3]{u}\,du = \int_{0}^{8}u^{\frac{4}{3}}\,du - (2+k)\int_{0}^{8}u^{\frac{1}{3}}\,du = \int_{0}^{8}\left(u - 2 - k\right)\sqrt[3]{u}\,du = \int_{0}^{8}u^{\frac{4}{3}}\,du - (2+k)\int_{0}^{8}u^{\frac{1}{3}}\,du](/latexrender/pictures/798764d656780fd7336cc78077184858.png)
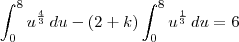





 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.