Agradeço pelo auxílio de todos... Voltando ao assunto...!
O seguinte limite está para ser calculado:
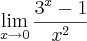
De acordo com minhas tentativas, não existe limite desta função no ponto 0, pois
 , segue o que fiz:
, segue o que fiz: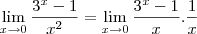
Elimino o limite fundamental, que é igual a
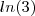 , porém
, porém  não tem limites laterais iguais, portanto não há limites, correto?
não tem limites laterais iguais, portanto não há limites, correto?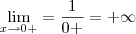

Porém no gabarito (não sei de qual livro), a professora colocou a resposta como
 , há essa possibilidade?
, há essa possibilidade?Grande abraço à todos.


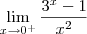 .
.