achar as assintotas verticais e horizontais e esboçar? o grafico....
f{x}=-3x/raiz de x^2-3
nao consigo achar a resposta nem um meio de chegar nela,,eu acho assistota vertical raiz de 3 mas a resposta e 3.
vlw pessoal



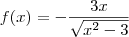 .
.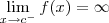
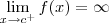
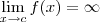
 aqui nesse caso pode representar tanto
aqui nesse caso pode representar tanto  quanto
quanto  .
.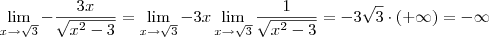
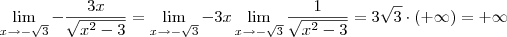
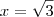 e
e  são assíntotas verticais do gráfico de f.
são assíntotas verticais do gráfico de f.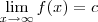
 aqui nesse caso pode representar tanto
aqui nesse caso pode representar tanto  quanto
quanto  .
.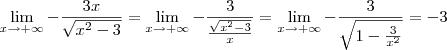
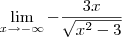
 ), podemos reescrever esse limite como:
), podemos reescrever esse limite como: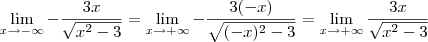
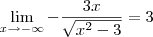
 e
e 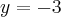 são assíntotas horizontais do gráfico de f.
são assíntotas horizontais do gráfico de f.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes

 .
.
 :
: