



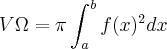
![f(x)=\sqrt[]{r^2-x^2} f(x)=\sqrt[]{r^2-x^2}](/latexrender/pictures/512e6c2f99df444d176d74da926b0931.png) , mas não sei se esta certa a função e também não sei como aplica-lá creio q o sólido seja conforme o anexo
, mas não sei se esta certa a função e também não sei como aplica-lá creio q o sólido seja conforme o anexo

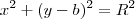 . Como o ponto
. Como o ponto 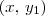 faz parte dessa circunferência, temos que
faz parte dessa circunferência, temos que 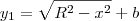 .
.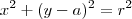 . Como o ponto
. Como o ponto 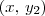 faz parte dessa circunferência, temos que
faz parte dessa circunferência, temos que  .
.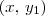 em torno do eixo x, a sua trajetória formará uma circunferência de raio
em torno do eixo x, a sua trajetória formará uma circunferência de raio  . Portanto, a área dessa circunferência será
. Portanto, a área dessa circunferência será 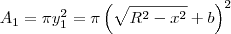 .
.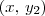 em torno do eixo x, a sua trajetória formará uma circunferência de raio
em torno do eixo x, a sua trajetória formará uma circunferência de raio  . Portanto, a área dessa circunferência será
. Portanto, a área dessa circunferência será 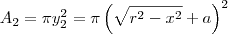 .
. e raio interno
e raio interno  . A área dessa coroa em função de x será
. A área dessa coroa em função de x será 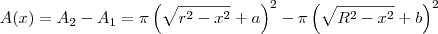 .
.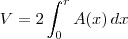 .
.

marciosouza escreveu:Olá, mas o intervalo não seria deaté
?

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.