 por Natalie » Ter Set 13, 2011 16:43
por Natalie » Ter Set 13, 2011 16:43
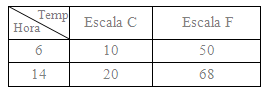
As escalas de temperatura Celsius (C) e Farenheit (F) são relacionadas pela função afim F = aC + b, onde a e b são constantes, F é a medida da temperatura na escala Farenheit e C é a medida da temperatura na escala Celsius. Num determinado dia, fizeram-se as seguintes medidas de temperatura mostradas na tabela a seguir, nos horários indicados.
Com esses dados, pode-se afirmar que os valores que correspondem a uma mesma temperatura são, respectivamente,
a) 30oC e 90oF
b) 25oC e 77oF
c) 24oC e 77oF
d) 15oC e 60oF
e) 12oC e 55oF
- Anexos
-
- Peies_I-dez-2002_-_Microsoft_Word_4.png (3.25 KiB) Exibido 3783 vezes
-
Natalie
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Set 13, 2011 16:25
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: cursinho pré vestibular
- Andamento: cursando
 por Neperiano » Ter Set 13, 2011 18:26
por Neperiano » Ter Set 13, 2011 18:26
Ola
Primeiro descubra o valor das constantes
Use o anexo para isso, você ira descobrir uma constante, a outra você tem porque você tem as horas, basta descobrir qual é qual
Mostre o que você fez
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Ter Set 13, 2011 19:28
por MarceloFantini » Ter Set 13, 2011 19:28
Você tentou usar a relação do problema e os dados da tabela para montar um sistema?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Natalie » Sex Set 16, 2011 17:14
por Natalie » Sex Set 16, 2011 17:14
Nao consegui obter a resposta
-
Natalie
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Set 13, 2011 16:25
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: cursinho pré vestibular
- Andamento: cursando
 por MarceloFantini » Sex Set 16, 2011 17:19
por MarceloFantini » Sex Set 16, 2011 17:19
Mostre o que você tentou.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Natalie » Sex Set 16, 2011 17:39
por Natalie » Sex Set 16, 2011 17:39
50=a.10 + b
68=a.20 +b
-
Natalie
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Set 13, 2011 16:25
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: cursinho pré vestibular
- Andamento: cursando
 por MarceloFantini » Sex Set 16, 2011 17:43
por MarceloFantini » Sex Set 16, 2011 17:43
Está certo. Quais foram os valores que você encontrou?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Natalie » Sex Set 16, 2011 17:51
por Natalie » Sex Set 16, 2011 17:51
a= 9/5
b= 32
-
Natalie
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Set 13, 2011 16:25
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: cursinho pré vestibular
- Andamento: cursando
 por MarceloFantini » Sex Set 16, 2011 17:56
por MarceloFantini » Sex Set 16, 2011 17:56
Estão certos. Usando eles, você testou as alternativas?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Sex Set 16, 2011 17:58
por Neperiano » Sex Set 16, 2011 17:58
Ola
50=a.10 + b
68=a.20 +b
Multiplica a segunda por -1, fica
50=10a+b
-68=-20a-b
-18=-10a
Logo a =18/10, ou 9/5
E b igual
50=10x9/5+b
50=18+b
b=32
Ou seja está correto seus valores, agora aplica na equação lá de cima, fica
F=9/5.C + 32, e vá tentando alternativa por alternativa até alguma der
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3429 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4199 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [Funções] questões de funções
por Zandrojr » Qua Ago 31, 2011 11:39
- 0 Respostas
- 3141 Exibições
- Última mensagem por Zandrojr

Qua Ago 31, 2011 11:39
Funções
-
- Funções
por Revelants » Dom Out 05, 2008 15:07
- 1 Respostas
- 3392 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Funçoes
por Luna » Seg Set 28, 2009 20:02
- 1 Respostas
- 2998 Exibições
- Última mensagem por Marcampucio

Seg Set 28, 2009 21:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.