 por Megatron32 » Ter Set 13, 2011 14:34
por Megatron32 » Ter Set 13, 2011 14:34
-
Megatron32
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Set 13, 2011 14:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia mecanica
- Andamento: cursando
 por LuizAquino » Ter Set 13, 2011 18:12
por LuizAquino » Ter Set 13, 2011 18:12
Eu vou fazer uma delas e você tenta o restante.
Vamos considerar que y é função de x. Ou seja, podemos escrever que y = f(x).
Então a função implícita
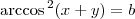
pode ser vista como

.
Note que temos uma composição de três funções. Por exemplo, considere que:
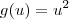
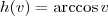
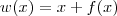
Com isso, a equação pode ser reescrita como g(h(w(x))) = b. Precisamos aplicar a regra da cadeia para calcular a derivada.
![[g(h(w(x)))]^\prime = b^\prime [g(h(w(x)))]^\prime = b^\prime](/latexrender/pictures/415114119bbf40f91d6cb918dcf6e461.png)
![g^\prime(h(w(x)))[h(w(x))]^\prime = 0 g^\prime(h(w(x)))[h(w(x))]^\prime = 0](/latexrender/pictures/5d08a00d13fc469d575e8906dfd68915.png)
![g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0 g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0](/latexrender/pictures/45b212da56bb746a35204f8974074c46.png)
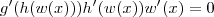
Calculando a derivada de cada função separadamente, sabemos que
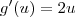
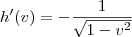
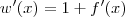
Agora, fazendo as substituições temos que:
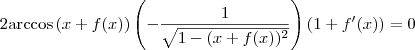
Lembrando que

e
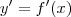
, ficamos com
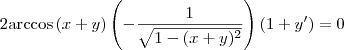 Observação
ObservaçãoSe você precisar revisar os conceitos de regra da cadeia e derivada de função implícita, então veja se as
vídeo-aulas "13. Cálculo I - Regra da Cadeia" e "14. Cálculo I - Derivada de Função Implícita" podem lhe ajudar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivação implicita , quem ajuda ?
por Loretto » Ter Ago 03, 2010 02:15
- 4 Respostas
- 5099 Exibições
- Última mensagem por LuizAquino

Qua Mar 09, 2011 22:03
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Função Implicita
por fabriel » Sex Mar 15, 2013 13:27
- 1 Respostas
- 1529 Exibições
- Última mensagem por e8group

Sex Mar 15, 2013 21:50
Cálculo: Limites, Derivadas e Integrais
-
- Função implícita; Questão complicada!
por jemourafer » Qui Mai 17, 2012 18:30
- 4 Respostas
- 4242 Exibições
- Última mensagem por Fabio Wanderley

Sáb Mai 19, 2012 03:16
Cálculo: Limites, Derivadas e Integrais
-
- Função de uma variavel (cartesiana, paramétrica e implícita)
por rhmgh » Dom Ago 12, 2012 21:20
- 3 Respostas
- 1806 Exibições
- Última mensagem por MarceloFantini

Qua Ago 15, 2012 10:27
Funções
-
- [Derivada] Função Implicita-duvidas na resoluão.
por fabriel » Dom Mar 17, 2013 01:11
- 3 Respostas
- 2076 Exibições
- Última mensagem por e8group

Dom Mar 17, 2013 14:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

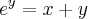



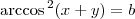 pode ser vista como
pode ser vista como  .
.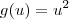
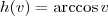
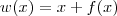
![[g(h(w(x)))]^\prime = b^\prime [g(h(w(x)))]^\prime = b^\prime](/latexrender/pictures/415114119bbf40f91d6cb918dcf6e461.png)
![g^\prime(h(w(x)))[h(w(x))]^\prime = 0 g^\prime(h(w(x)))[h(w(x))]^\prime = 0](/latexrender/pictures/5d08a00d13fc469d575e8906dfd68915.png)
![g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0 g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0](/latexrender/pictures/45b212da56bb746a35204f8974074c46.png)
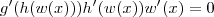
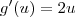
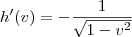
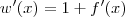
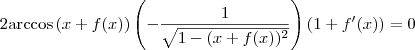
 e
e 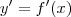 , ficamos com
, ficamos com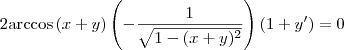



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.