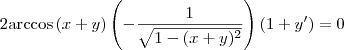Eu vou fazer uma delas e você tenta o restante.
Vamos considerar que y é função de x. Ou seja, podemos escrever que y = f(x).
Então a função implícita
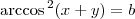
pode ser vista como

.
Note que temos uma composição de três funções. Por exemplo, considere que:
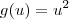
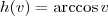
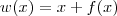
Com isso, a equação pode ser reescrita como g(h(w(x))) = b. Precisamos aplicar a regra da cadeia para calcular a derivada.
![[g(h(w(x)))]^\prime = b^\prime [g(h(w(x)))]^\prime = b^\prime](/latexrender/pictures/415114119bbf40f91d6cb918dcf6e461.png)
![g^\prime(h(w(x)))[h(w(x))]^\prime = 0 g^\prime(h(w(x)))[h(w(x))]^\prime = 0](/latexrender/pictures/5d08a00d13fc469d575e8906dfd68915.png)
![g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0 g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0](/latexrender/pictures/45b212da56bb746a35204f8974074c46.png)
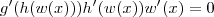
Calculando a derivada de cada função separadamente, sabemos que
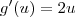
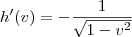
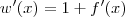
Agora, fazendo as substituições temos que:
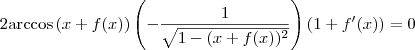
Lembrando que

e
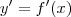
, ficamos com
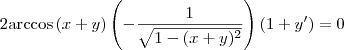 Observação
ObservaçãoSe você precisar revisar os conceitos de regra da cadeia e derivada de função implícita, então veja se as
vídeo-aulas "13. Cálculo I - Regra da Cadeia" e "14. Cálculo I - Derivada de Função Implícita" podem lhe ajudar.

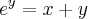



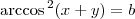 pode ser vista como
pode ser vista como  .
.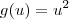
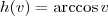
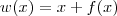
![[g(h(w(x)))]^\prime = b^\prime [g(h(w(x)))]^\prime = b^\prime](/latexrender/pictures/415114119bbf40f91d6cb918dcf6e461.png)
![g^\prime(h(w(x)))[h(w(x))]^\prime = 0 g^\prime(h(w(x)))[h(w(x))]^\prime = 0](/latexrender/pictures/5d08a00d13fc469d575e8906dfd68915.png)
![g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0 g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0](/latexrender/pictures/45b212da56bb746a35204f8974074c46.png)
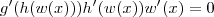
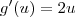
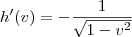
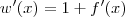
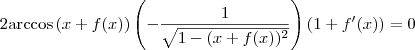
 e
e 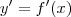 , ficamos com
, ficamos com