 por nicolascalcagnoto » Qua Set 07, 2011 20:29
por nicolascalcagnoto » Qua Set 07, 2011 20:29
Boa Noite, Gostaria de uma breve analise para ver se estou fazendo corretamente.
1) Esboce o gráfico das seguintes funções exponenciais, sendo f: IR -> IR
Utilizar os numeros para X( -2, -1, 0, 1, 2 )
a)
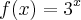
b)

c)

d

e)

Obrigado, eu comecei fazendo assim, vou por a letra A

Obrigado
Editado pela última vez por
nicolascalcagnoto em Qui Set 08, 2011 03:20, em um total de 4 vezes.
-
nicolascalcagnoto
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Set 07, 2011 20:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias Contabeis
- Andamento: cursando
 por MarceloFantini » Qua Set 07, 2011 21:03
por MarceloFantini » Qua Set 07, 2011 21:03
Quando o expoente é negativo, temos

, então

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nicolascalcagnoto » Qua Set 07, 2011 21:13
por nicolascalcagnoto » Qua Set 07, 2011 21:13
MarceloFantini escreveu:Quando o expoente é negativo, temos

, então

.
huum, entenedi, muito obrigado
agora so tenho duvida na letra E
-
nicolascalcagnoto
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Set 07, 2011 20:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias Contabeis
- Andamento: cursando
 por MarceloFantini » Qua Set 07, 2011 21:17
por MarceloFantini » Qua Set 07, 2011 21:17
Qual é a sua dúvida?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nicolascalcagnoto » Qua Set 07, 2011 21:22
por nicolascalcagnoto » Qua Set 07, 2011 21:22
MarceloFantini escreveu:Qual é a sua dúvida?
resolvendo a letra E ficaria assim
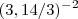
depois disso como faz? e o valor de pi so deixo 3,14?
-
nicolascalcagnoto
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Set 07, 2011 20:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias Contabeis
- Andamento: cursando
 por MarceloFantini » Qua Set 07, 2011 21:28
por MarceloFantini » Qua Set 07, 2011 21:28
Perceba que elevar a um expoente negativo é inverter a fração. Não se preocupe com valores aproximados, apenas perceba que
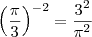
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nicolascalcagnoto » Qua Set 07, 2011 21:47
por nicolascalcagnoto » Qua Set 07, 2011 21:47
MarceloFantini escreveu:Perceba que elevar a um expoente negativo é inverter a fração. Não se preocupe com valores aproximados, apenas perceba que
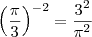
.
ok
Editado pela última vez por
nicolascalcagnoto em Qui Set 08, 2011 03:18, em um total de 1 vez.
-
nicolascalcagnoto
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Set 07, 2011 20:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias Contabeis
- Andamento: cursando
 por nicolascalcagnoto » Qua Set 07, 2011 22:15
por nicolascalcagnoto » Qua Set 07, 2011 22:15
Isso esta certo?
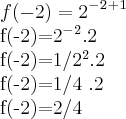
-
nicolascalcagnoto
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Set 07, 2011 20:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias Contabeis
- Andamento: cursando
 por MarceloFantini » Qua Set 07, 2011 22:18
por MarceloFantini » Qua Set 07, 2011 22:18
Está.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nicolascalcagnoto » Qui Set 08, 2011 00:56
por nicolascalcagnoto » Qui Set 08, 2011 00:56
-
nicolascalcagnoto
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Set 07, 2011 20:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias Contabeis
- Andamento: cursando
 por MarceloFantini » Qui Set 08, 2011 01:23
por MarceloFantini » Qui Set 08, 2011 01:23
Estão certas. E deixe como está, ficará

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nicolascalcagnoto » Qui Set 08, 2011 01:37
por nicolascalcagnoto » Qui Set 08, 2011 01:37
MarceloFantini escreveu:Estão certas. E deixe como está, ficará

.
a sim, muito obrigado acabou minhas duvidas, o resto ja fiz tudo.
Att; Nicolas
-
nicolascalcagnoto
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Set 07, 2011 20:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias Contabeis
- Andamento: cursando
 por nicolaspsy » Qui Set 08, 2011 16:32
por nicolaspsy » Qui Set 08, 2011 16:32
É assim que se faz?
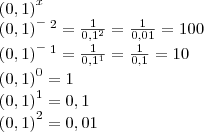
-
nicolaspsy
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Set 08, 2011 03:24
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por nicolaspsy » Qui Set 08, 2011 16:55
por nicolaspsy » Qui Set 08, 2011 16:55
Para que valores de k a função

é decrescente?
Alguem poderia me explicar? não entendi, parece simples mas... rs
teria que ter dois valores não é? um para X e um para K
para saber quando é decrescente.
vamos adotar os numeros -2,-1,0,1,2 para X
-
nicolaspsy
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Set 08, 2011 03:24
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Qui Set 08, 2011 18:36
por MarceloFantini » Qui Set 08, 2011 18:36
Considere
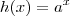
. Esta função será crescente se
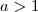
e decrescente se
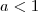
. Tente resolver usando isso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nicolaspsy » Sáb Set 10, 2011 13:23
por nicolaspsy » Sáb Set 10, 2011 13:23
MarceloFantini escreveu:Considere
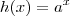
. Esta função será crescente se
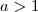
e decrescente se
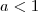
. Tente resolver usando isso.
intão o valor de x deve ser x<1 mas e o valor de K ? tambem seria menor do que 1 ? :s
não entendi
-
nicolaspsy
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Set 08, 2011 03:24
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por phvicari » Sáb Set 10, 2011 18:38
por phvicari » Sáb Set 10, 2011 18:38
-
phvicari
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Set 03, 2011 04:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por nicolaspsy » Sáb Set 10, 2011 20:27
por nicolaspsy » Sáb Set 10, 2011 20:27
Continuo sem intenger, caso o k<4. Utilizei o k sendo 3 veja como ficou nao vai ser descrecente :s

ou nesse caso so uso valores menores do que 1 para x? no caso x=1 x=0/ x-1
-
nicolaspsy
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Set 08, 2011 03:24
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Sáb Set 10, 2011 20:36
por MarceloFantini » Sáb Set 10, 2011 20:36
Nicolas, o caso

não foi considerado em nenhum dos posts anteriores justamente pela série de problemas que traz. A idéia intuitiva é que quando se eleva um número menor que 1 a um expoente, a medida que o expoente cresce este número torna-se cada vez mais próximo de zero, ao passo que quando um número maior que um é elevado a um expoente, este torna-se cada vez maior sem se aproximar de um valor fixo, por isso infinito. Além do mais, note que o primeiro caso é estritamente decrescente e o segundo estritamente crescente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nicolaspsy » Dom Set 11, 2011 13:28
por nicolaspsy » Dom Set 11, 2011 13:28
MarceloFantini escreveu:Nicolas, o caso

não foi considerado em nenhum dos posts anteriores justamente pela série de problemas que traz. A idéia intuitiva é que quando se eleva um número menor que 1 a um expoente, a medida que o expoente cresce este número torna-se cada vez mais próximo de zero, ao passo que quando um número maior que um é elevado a um expoente, este torna-se cada vez maior sem se aproximar de um valor fixo, por isso infinito. Além do mais, note que o primeiro caso é estritamente decrescente e o segundo estritamente crescente.
huum, agora entendi o pensamento, obrigado
-
nicolaspsy
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Set 08, 2011 03:24
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por nicolaspsy » Qui Set 15, 2011 00:48
por nicolaspsy » Qui Set 15, 2011 00:48
nicolaspsy escreveu:MarceloFantini escreveu:Nicolas, o caso

não foi considerado em nenhum dos posts anteriores justamente pela série de problemas que traz. A idéia intuitiva é que quando se eleva um número menor que 1 a um expoente, a medida que o expoente cresce este número torna-se cada vez mais próximo de zero, ao passo que quando um número maior que um é elevado a um expoente, este torna-se cada vez maior sem se aproximar de um valor fixo, por isso infinito. Além do mais, note que o primeiro caso é estritamente decrescente e o segundo estritamente crescente.
huum, agora entendi o pensamento, obrigado
a respota final então seria ]3,4[
certo?

-
nicolaspsy
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Set 08, 2011 03:24
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Qui Set 15, 2011 16:00
por MarceloFantini » Qui Set 15, 2011 16:00
Certo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- funções exponenciais
por simas4387 » Qua Nov 24, 2010 16:40
- 1 Respostas
- 2047 Exibições
- Última mensagem por simas4387

Sex Dez 03, 2010 18:46
Funções
-
- [Funções Exponenciais]
por nicolaspsy » Ter Set 20, 2011 02:05
- 1 Respostas
- 1814 Exibições
- Última mensagem por MarceloFantini

Qua Set 21, 2011 21:42
Funções
-
- Funcoes exponenciais
por Petrincha » Dom Jan 15, 2012 19:51
- 8 Respostas
- 4950 Exibições
- Última mensagem por Petrincha

Dom Jan 15, 2012 20:51
Funções
-
- [Funções exponenciais] Exercícios
por Texas » Qui Set 22, 2011 16:34
- 3 Respostas
- 2223 Exibições
- Última mensagem por MarceloFantini

Qui Set 22, 2011 19:23
Funções
-
- Derivadas de funções Exponenciais
por Ana Maria da Silva » Dom Jun 30, 2013 13:33
- 3 Respostas
- 4174 Exibições
- Última mensagem por Molina

Sex Jul 12, 2013 22:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
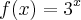






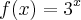







, então
.


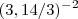 depois disso como faz? e o valor de pi so deixo 3,14?
depois disso como faz? e o valor de pi so deixo 3,14?
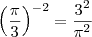 .
.

.

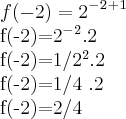







![f(x)=\left(\sqrt[2]{2} \right)^x
f(-2)=\left(\sqrt[2]{2} \right)^-^2
f(-2)=\left({2}^{\frac{1}{2}} \right)^-^2
f(-2)=\left({2}^{-\frac{2}{2}} \right)
f(-2)= 2^-^1
f(-2)=\left( \frac{1}{2} \right)
-----------------------
f(-1)=\left(\sqrt[2]{2} \right)^-^1
f(-1)=\left({2}^{\frac{1}{2}} \right)^-^1
f(-1)=\left({2}^{-\frac{1}{2}} \right)
f(-1)=\left(\frac{1}{2^\frac{1}{2}} \right) f(x)=\left(\sqrt[2]{2} \right)^x
f(-2)=\left(\sqrt[2]{2} \right)^-^2
f(-2)=\left({2}^{\frac{1}{2}} \right)^-^2
f(-2)=\left({2}^{-\frac{2}{2}} \right)
f(-2)= 2^-^1
f(-2)=\left( \frac{1}{2} \right)
-----------------------
f(-1)=\left(\sqrt[2]{2} \right)^-^1
f(-1)=\left({2}^{\frac{1}{2}} \right)^-^1
f(-1)=\left({2}^{-\frac{1}{2}} \right)
f(-1)=\left(\frac{1}{2^\frac{1}{2}} \right)](/latexrender/pictures/d35278d078fa7a3672364f2246c5bbdb.png)


.

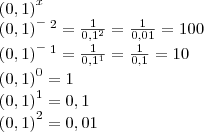

 é decrescente?
é decrescente?
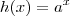 . Esta função será crescente se
. Esta função será crescente se 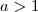 e decrescente se
e decrescente se 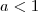 . Tente resolver usando isso.
. Tente resolver usando isso.

. Esta função será crescente se
e decrescente se
. Tente resolver usando isso.

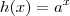
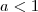

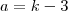
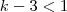
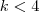



 não foi considerado em nenhum dos posts anteriores justamente pela série de problemas que traz. A idéia intuitiva é que quando se eleva um número menor que 1 a um expoente, a medida que o expoente cresce este número torna-se cada vez mais próximo de zero, ao passo que quando um número maior que um é elevado a um expoente, este torna-se cada vez maior sem se aproximar de um valor fixo, por isso infinito. Além do mais, note que o primeiro caso é estritamente decrescente e o segundo estritamente crescente.
não foi considerado em nenhum dos posts anteriores justamente pela série de problemas que traz. A idéia intuitiva é que quando se eleva um número menor que 1 a um expoente, a medida que o expoente cresce este número torna-se cada vez mais próximo de zero, ao passo que quando um número maior que um é elevado a um expoente, este torna-se cada vez maior sem se aproximar de um valor fixo, por isso infinito. Além do mais, note que o primeiro caso é estritamente decrescente e o segundo estritamente crescente.

não foi considerado em nenhum dos posts anteriores justamente pela série de problemas que traz. A idéia intuitiva é que quando se eleva um número menor que 1 a um expoente, a medida que o expoente cresce este número torna-se cada vez mais próximo de zero, ao passo que quando um número maior que um é elevado a um expoente, este torna-se cada vez maior sem se aproximar de um valor fixo, por isso infinito. Além do mais, note que o primeiro caso é estritamente decrescente e o segundo estritamente crescente.

não foi considerado em nenhum dos posts anteriores justamente pela série de problemas que traz. A idéia intuitiva é que quando se eleva um número menor que 1 a um expoente, a medida que o expoente cresce este número torna-se cada vez mais próximo de zero, ao passo que quando um número maior que um é elevado a um expoente, este torna-se cada vez maior sem se aproximar de um valor fixo, por isso infinito. Além do mais, note que o primeiro caso é estritamente decrescente e o segundo estritamente crescente.



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
