1) Esboce o gráfico das seguintes funções exponenciais, sendo f: IR -> IR
Utilizar os numeros para X( -2, -1, 0, 1, 2 )
a)
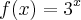
b)

c)

d

e)

Obrigado, eu comecei fazendo assim, vou por a letra A

Obrigado

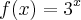







MarceloFantini escreveu:Quando o expoente é negativo, temos, então
.


MarceloFantini escreveu:Qual é a sua dúvida?
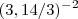 depois disso como faz? e o valor de pi so deixo 3,14?
depois disso como faz? e o valor de pi so deixo 3,14?
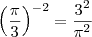 .
.

MarceloFantini escreveu:Perceba que elevar a um expoente negativo é inverter a fração. Não se preocupe com valores aproximados, apenas perceba que.

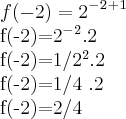







![f(x)=\left(\sqrt[2]{2} \right)^x
f(-2)=\left(\sqrt[2]{2} \right)^-^2
f(-2)=\left({2}^{\frac{1}{2}} \right)^-^2
f(-2)=\left({2}^{-\frac{2}{2}} \right)
f(-2)= 2^-^1
f(-2)=\left( \frac{1}{2} \right)
-----------------------
f(-1)=\left(\sqrt[2]{2} \right)^-^1
f(-1)=\left({2}^{\frac{1}{2}} \right)^-^1
f(-1)=\left({2}^{-\frac{1}{2}} \right)
f(-1)=\left(\frac{1}{2^\frac{1}{2}} \right) f(x)=\left(\sqrt[2]{2} \right)^x
f(-2)=\left(\sqrt[2]{2} \right)^-^2
f(-2)=\left({2}^{\frac{1}{2}} \right)^-^2
f(-2)=\left({2}^{-\frac{2}{2}} \right)
f(-2)= 2^-^1
f(-2)=\left( \frac{1}{2} \right)
-----------------------
f(-1)=\left(\sqrt[2]{2} \right)^-^1
f(-1)=\left({2}^{\frac{1}{2}} \right)^-^1
f(-1)=\left({2}^{-\frac{1}{2}} \right)
f(-1)=\left(\frac{1}{2^\frac{1}{2}} \right)](/latexrender/pictures/d35278d078fa7a3672364f2246c5bbdb.png)


MarceloFantini escreveu:Estão certas. E deixe como está, ficará.

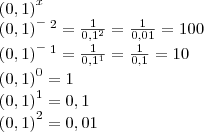

 é decrescente?
é decrescente?
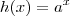 . Esta função será crescente se
. Esta função será crescente se 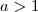 e decrescente se
e decrescente se 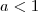 . Tente resolver usando isso.
. Tente resolver usando isso.

MarceloFantini escreveu:Considere. Esta função será crescente se
e decrescente se
. Tente resolver usando isso.

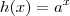
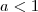

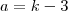
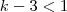
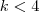

phvicari escreveu:
Para ser decrescente temos que:
Analogamente, na função mostrada por vecê temos:


 não foi considerado em nenhum dos posts anteriores justamente pela série de problemas que traz. A idéia intuitiva é que quando se eleva um número menor que 1 a um expoente, a medida que o expoente cresce este número torna-se cada vez mais próximo de zero, ao passo que quando um número maior que um é elevado a um expoente, este torna-se cada vez maior sem se aproximar de um valor fixo, por isso infinito. Além do mais, note que o primeiro caso é estritamente decrescente e o segundo estritamente crescente.
não foi considerado em nenhum dos posts anteriores justamente pela série de problemas que traz. A idéia intuitiva é que quando se eleva um número menor que 1 a um expoente, a medida que o expoente cresce este número torna-se cada vez mais próximo de zero, ao passo que quando um número maior que um é elevado a um expoente, este torna-se cada vez maior sem se aproximar de um valor fixo, por isso infinito. Além do mais, note que o primeiro caso é estritamente decrescente e o segundo estritamente crescente.

MarceloFantini escreveu:Nicolas, o casonão foi considerado em nenhum dos posts anteriores justamente pela série de problemas que traz. A idéia intuitiva é que quando se eleva um número menor que 1 a um expoente, a medida que o expoente cresce este número torna-se cada vez mais próximo de zero, ao passo que quando um número maior que um é elevado a um expoente, este torna-se cada vez maior sem se aproximar de um valor fixo, por isso infinito. Além do mais, note que o primeiro caso é estritamente decrescente e o segundo estritamente crescente.

nicolaspsy escreveu:MarceloFantini escreveu:Nicolas, o casonão foi considerado em nenhum dos posts anteriores justamente pela série de problemas que traz. A idéia intuitiva é que quando se eleva um número menor que 1 a um expoente, a medida que o expoente cresce este número torna-se cada vez mais próximo de zero, ao passo que quando um número maior que um é elevado a um expoente, este torna-se cada vez maior sem se aproximar de um valor fixo, por isso infinito. Além do mais, note que o primeiro caso é estritamente decrescente e o segundo estritamente crescente.
huum, agora entendi o pensamento, obrigado



Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.
 :
: