Estou tentando montar as equações do seguinte problema, mas não estou conseguindo. Gostaria da ajuda de um dos colegas.
Um grupo de jovens alugou um onibus para uma excursão. Cada um dos jovens pagou o mesmo valor para o aluguel do onibus. Se no grupo houvesse 20 jovens a mais cada um pagaria R$ 40,00 a menos. Se houvessem 3 jovens a menos cada um pagaria R$ 12,00 a mais. qual o valor pago por cada um dos jovens?
Considerei x= nº de jovens e y-valor pago por cada jovem.
Tentei desta forma, porem não deu o valor do resultado ( R$92,00)
x+20 = y-40,00
x-3=y+12


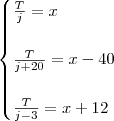

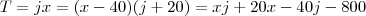 e
e 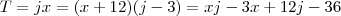 , ou seja:
, ou seja:



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)