 [f(4 + h)- f(4)]/h
[f(4 + h)- f(4)]/hsendo f(x)=4x² + 3
sendo assim, f(4)=67.
Assim, o limite nao existiria, pelo fato de o numerador (67-0) - (67) e o denominador derem zero?

 [f(4 + h)- f(4)]/h
[f(4 + h)- f(4)]/h
isanobile escreveu:sendo assim, f(4)=67.
Assim, o limite nao existiria, pelo fato de o numerador (67-0) - (67) e o denominador derem zero?
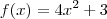 :
: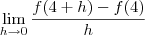
![\lim_{h\to 0} \frac{[4(4+h)^2 + 3] - (4\cdot 4^2 + 3)}{h} \lim_{h\to 0} \frac{[4(4+h)^2 + 3] - (4\cdot 4^2 + 3)}{h}](/latexrender/pictures/2290b707a76ebccd45682ef16d5356bd.png)


![\lim_{\rightarrow 0} [4(4+h)² + 3] - 4(4)²+3/h \lim_{\rightarrow 0} [4(4+h)² + 3] - 4(4)²+3/h](/latexrender/pictures/eefd3d586fd988a40913ef06ed65fece.png)
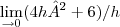

isanobile escreveu:Entendi o raciocínio, mas nao entendi o 32h .
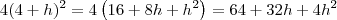
isanobile escreveu:Meu resultado a partir de
foi :
isanobile escreveu:e como eu terminaria? Tentei fatorar esse ultimo resultado tirando as raizes por Baskara mas travei novamente.
isanobile escreveu:Obs: desconsidere esse  que aparece ao quadrado, era para ser um "H", mas quando digitei o limite no editor de formulas apareceu isso.
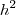 .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes

 .
.
 :
: