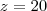por andregoulart » Seg Mar 09, 2009 15:53
por andregoulart » Seg Mar 09, 2009 15:53
Numa pesquisa de intenção de votos, em que as pessoas deveriam responder sim ou não, foram feitas as seguintes perguntas;
1) Voce votou no atual prefeito?
2) Se o atual prefeito fosse candidato à reeleição, não votaria nele?
Nenhuma pergunta ficou sem resposta, 30 pessoas responderam sim as duas questões, 60 responderam não a primeira questão, 80 responderam não a segunda questão e 130 disseram sim a uma questão, ao menos. O número de pessoas entrevistadas foi de?
RESPOSTA: 150
Tentei fazer pelo diagrama de Venn e pela fórmula n(AUB)= N(A)+ N(B)- N(AUB) e até cheguei na resposta, mais não convenceu e preciso de uma resolução melhor. Alguém pode me ajudar nas dicas????
-
andregoulart
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Mar 09, 2009 15:08
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por Marcampucio » Sex Mar 13, 2009 17:04
por Marcampucio » Sex Mar 13, 2009 17:04
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por andregoulart » Sex Mar 13, 2009 17:16
por andregoulart » Sex Mar 13, 2009 17:16
Se separarmos pelo diagrama de VENN em sim ou não, temos que.
30 pessoas responderam sim as duas questões e 130 sim a uma questão ao menos.
pergunta 1- x pergunta 2-y, portanto X+y+30= 130 e x+y= 100 (1)
Por outro lado
60 responderam não a primeira questão (y) e 80 não a segunda questão(x) e z não a ambas as questões, assim
x+z= 80 y+z=60 , resolvendo o sistema , temos que x-y=20 e fazendo o sistema com x+y=100 (1) , encontramos x=60, y=40, z=20
Então,
x+y+z+30= 60+40+20+30= 150 entrevistados.
-
andregoulart
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Mar 09, 2009 15:08
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8842 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Teoria dos conjuntos] Questão de conjuntos
por VitorFN » Qua Fev 14, 2018 01:07
- 1 Respostas
- 7828 Exibições
- Última mensagem por DarioCViveiros

Sex Fev 23, 2018 18:35
Conjuntos
-
- Teoria dos Conjuntos
por tertulia » Seg Dez 27, 2010 17:47
- 3 Respostas
- 3468 Exibições
- Última mensagem por Drakangt

Seg Dez 29, 2014 14:29
Álgebra Elementar
-
- Teoria dos conjuntos
por joseailton » Seg Mar 05, 2012 02:20
- 1 Respostas
- 1900 Exibições
- Última mensagem por timoteo

Seg Mar 05, 2012 09:32
Álgebra Elementar
-
- Teoria dos Conjuntos
por petras » Sex Jan 22, 2016 21:35
- 1 Respostas
- 2792 Exibições
- Última mensagem por DarioCViveiros

Sex Fev 23, 2018 18:51
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



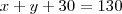
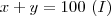
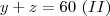
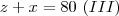
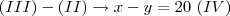
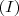 e
e  vem
vem 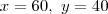 e logo
e logo