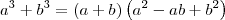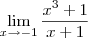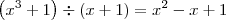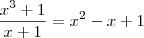por beel » Sex Set 02, 2011 16:19
por beel » Sex Set 02, 2011 16:19
PRA RESOLVER UM LIMITE, PRIMEIRO VC TENTA SUBSTITUIR O a em x...MAS SE O DENOMINADOR DER ZERO ( NAO O +/-)TEM QUE FATORAR CERTO?
MAS NESSE CASO, COMO EU RESOLVO?
lim x³+1/x+ 1
x TENDE a -1
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Sex Set 02, 2011 16:55
por Neperiano » Sex Set 02, 2011 16:55
Ola
Usa a regra de L'Hopital
Derive emcima e embaixo separadamente, e tente fazer o limite denovo
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por beel » Sex Set 02, 2011 17:04
por beel » Sex Set 02, 2011 17:04
QUE REGRA É ESSA? HAHA
NAO APRENDI A DERIVAR AINDA, TEM OUTRO JEITO DE RESOLVER?
POR ALGUMA FATORAÇÃO?
A UNICA QUE EU SEI QUE ENVOLVE CUBO, É A DA DIFERENÇA DE CUBOS, MAS NENHUMA RELATIVA A SOMA
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Sex Set 02, 2011 17:24
por LuizAquino » Sex Set 02, 2011 17:24
Use o produto notável:
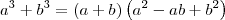
Outra alternativa seria simplesmente efetuar a divisão entre os polinômios. Se você não se recorda como efetuar essa divisão, então eu recomendo que você revise esse conteúdo.
ObservaçãoPara escrever limites em suas mensagens, use o botão "tex" disponível durante a edição. Por exemplo, para o limite que você enviou basta digitar o comando:
- Código: Selecionar todos
[tex]
\lim_{x\to -1} \frac{x^3 + 1}{x + 1}
[/tex]
O resultado desse comando após enviar sua mensagem seria:
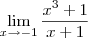
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Sex Set 02, 2011 17:47
por beel » Sex Set 02, 2011 17:47
NAO CONHECIA ESSA FORMULA DA SOMA DE DOIS CUBOS,
POR ELA, ACHO QUE CONSEGUIR RESOLVER, MEU LIMITE DEU 3
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por beel » Sex Set 02, 2011 17:48
por beel » Sex Set 02, 2011 17:48
A FORMULA DO POLINOMIO NAO É APENAS QUANDO O X TENDE AO INFINITO?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Sex Set 02, 2011 18:04
por LuizAquino » Sex Set 02, 2011 18:04
isanobile escreveu:ACHO QUE CONSEGUIR RESOLVER, MEU LIMITE DEU 3
Ok. Esse é o valor.
isanobile escreveu:A FORMULA DO POLINOMIO NAO É APENAS QUANDO O X TENDE AO INFINITO?
Você está se referindo a estratégia de dividir os polinômios? Se for isso, a resposta é não.
Veja que -1 é raiz tanto de d(x) = x³ + 1 quanto de n(x) = x + 1. Do conhecimento sobre divisão de polinômios, sabemos que isso significa que x³ + 1 é divisível por x + 1. Se você efetuar a divisão, então obtém:
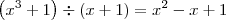
Em notação de fração, temos que:
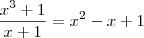
Veja que aplicando o conhecimento sobre divisão entre polinômios não é necessário gravar os produtos notáveis.
Entretanto é natural que com a prática acabamos gravando uma porção de produtos notáveis.
ObservaçãoPor favor,
não digite suas mensagens usando apenas caixa alta, isto é, com todas as letras em maiúsculo.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Dom Out 16, 2011 17:00
por beel » Dom Out 16, 2011 17:00
Ok,obrigada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo de Limite] Resolução de um limite
por julianocoutinho » Seg Mai 13, 2013 01:47
- 3 Respostas
- 3324 Exibições
- Última mensagem por Man Utd

Qua Mai 15, 2013 22:26
Cálculo: Limites, Derivadas e Integrais
-
- [Limite]Resolução do limite
por joaop_sjc » Ter Jul 02, 2013 17:22
- 2 Respostas
- 1591 Exibições
- Última mensagem por Leticia_alves

Sáb Jul 06, 2013 21:41
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] RESOLUÇÃO
por beel » Sex Set 02, 2011 15:14
- 2 Respostas
- 1713 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:03
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] RESOLUÇÃO 2
por beel » Sex Set 02, 2011 17:58
- 2 Respostas
- 1711 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:03
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] RESOLUÇÃO 3
por beel » Sáb Set 03, 2011 20:17
- 8 Respostas
- 4753 Exibições
- Última mensagem por beel

Dom Set 04, 2011 15:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.