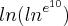
OBS: o e que esta elevado a 10 e o número de Euler..

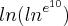

 , avise.
, avise. 


Guilherme Carvalho escreveu:O pior que isso mesmo, por isso estou achando estranho nunca vi isso não sei nem por onde começar
 .
.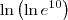 .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 .
.
 :
: