 por Guilherme Carvalho » Qui Set 01, 2011 21:27
por Guilherme Carvalho » Qui Set 01, 2011 21:27
galera me ajuda a achar o valor desta expressão por favor
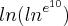
OBS: o e que esta elevado a 10 e o número de Euler..
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por Molina » Qui Set 01, 2011 22:21
por Molina » Qui Set 01, 2011 22:21
Boa noite, Guilherme.
Confirme, você escreveu dentro do parênteses ln elevado a
e,
e elevado a 10. Isso não faz muito sentido...
Caso você tenha tentado escrever

, avise.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Guilherme Carvalho » Sex Set 02, 2011 00:45
por Guilherme Carvalho » Sex Set 02, 2011 00:45
O pior que isso mesmo, por isso estou achando estranho nunca vi isso não sei nem por onde começar
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por LuizAquino » Sex Set 02, 2011 11:35
por LuizAquino » Sex Set 02, 2011 11:35
Guilherme Carvalho escreveu:O pior que isso mesmo, por isso estou achando estranho nunca vi isso não sei nem por onde começar
O que você escreveu originalmente é uma operação
inválida e portanto não pode ser calculada:

.
Se você viu
exatamente isso em algum lugar, então o mais provável é que houve um erro de digitação.
Por outro lado, a expressão que o colega Molina escreveu é uma operação
válida e portanto pode ser calculada:
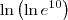
.
No caso, basta aplicar as regras de logaritmos:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda
por Daiane kelly » Seg Mar 24, 2008 22:38
- 4 Respostas
- 6390 Exibições
- Última mensagem por Cleyson007

Ter Mai 12, 2009 17:43
Matrizes e Determinantes
-
- Ajuda
por Umbus » Sáb Out 18, 2008 14:12
- 2 Respostas
- 3677 Exibições
- Última mensagem por lopes

Sáb Jun 20, 2009 15:51
Álgebra Linear
-
- Ajuda.
por VanessaFontela » Qui Dez 04, 2008 10:32
- 0 Respostas
- 2897 Exibições
- Última mensagem por VanessaFontela

Qui Dez 04, 2008 10:32
Matemática Financeira
-
- Ajuda!!!
por GABRIELA » Seg Set 21, 2009 17:28
- 1 Respostas
- 2289 Exibições
- Última mensagem por Molina

Seg Set 21, 2009 19:56
Sistemas de Equações
-
- Ajuda!!!!!!
por GABRIELA » Ter Set 22, 2009 16:35
- 6 Respostas
- 4424 Exibições
- Última mensagem por GABRIELA

Qui Set 24, 2009 16:29
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
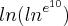

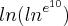

 , avise.
, avise. 


 .
.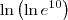 .
.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.