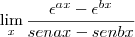 ( lembrando o x está tendendo a zero)
( lembrando o x está tendendo a zero)tentei dividir tudo por senax+senbx mas não consegui, tentei fazendo
 mas não consegui sair disso alguem me explique como resolver obrigado.
mas não consegui sair disso alguem me explique como resolver obrigado.
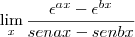 ( lembrando o x está tendendo a zero)
( lembrando o x está tendendo a zero) mas não consegui sair disso alguem me explique como resolver obrigado.
mas não consegui sair disso alguem me explique como resolver obrigado.
 .
.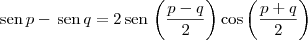 .
.
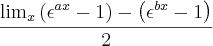 =
= 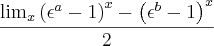 =
= 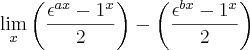

matmatco escreveu:usei a identidade e encontrei uma resposta igual a 2, ai voltando ao limite ficou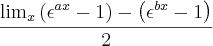
![\lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\textrm{sen}\,ax - \,\textrm{sen}\,bx} = \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{2\,\textrm{sen}\,\left[\frac{(a-b)x}{2}\right]\cos\left[\frac{(a+b)x}{2}\right]} \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\textrm{sen}\,ax - \,\textrm{sen}\,bx} = \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{2\,\textrm{sen}\,\left[\frac{(a-b)x}{2}\right]\cos\left[\frac{(a+b)x}{2}\right]}](/latexrender/pictures/e7c8ff071ee7b218a291aaf66a12f15c.png)
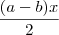 (lembrando que devemos ter
(lembrando que devemos ter  ), ficamos com
), ficamos com![\lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\textrm{sen}\,ax - \,\textrm{sen}\,bx} = \lim_{x\to 0}\frac{\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\frac{(a-b)x}{2}}}{\frac{2\,\textrm{sen}\,\left[\frac{(a-b)x}{2}\right]\cos\left[\frac{(a+b)x}{2}\right]}{\frac{(a-b)x}{2}}} = \frac{1}{a-b} \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{x} \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\textrm{sen}\,ax - \,\textrm{sen}\,bx} = \lim_{x\to 0}\frac{\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\frac{(a-b)x}{2}}}{\frac{2\,\textrm{sen}\,\left[\frac{(a-b)x}{2}\right]\cos\left[\frac{(a+b)x}{2}\right]}{\frac{(a-b)x}{2}}} = \frac{1}{a-b} \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{x}](/latexrender/pictures/2d09537aeb33be1ee013e4e7d41ad30f.png)

x \to 0
 .
. , usamos o comando LaTeX:
, usamos o comando LaTeX:\lim_{x\to a} f(x)
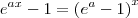 .
.

nietzsche escreveu:luiz,
se a= 0 a observação 2 é correta.

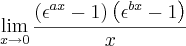 ae já está resolvido o problema
ae já está resolvido o problema 
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)