nietzsche escreveu:Queremos provar que dado

> 0, existe m>0, tal que,
se n > m, então

. (*)
Ok. Mas o abuso de notação com a igualdade pode confundir. Pode dar a impressão de que

ao invés de

como diz o exercício. Eu acredito que seria mais interessante colocar apenas
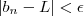
.
nietzsche escreveu:Sabemos que para todo

> 0, existe M>0, tal que,
se n > M, então
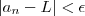
.
Ok.
nietzsche escreveu:Como
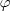
é uma bijeção, temos uma correspondência um a um entre

e n, para todo n natural.
Ok.
nietzsche escreveu:Ou seja que

e an tem o mesmo número de termos.
Ok.
nietzsche escreveu:Tomando m = M teremos que a partir de n>M a linha (*) acontece (...)
Aqui há um problema. Veja que na bijeção
 nada garante
nada garante que se i < j temos

. Nesse caso, nem todos os termos a partir de M necessariamente tornam (*) verdadeira.
Vamos então dividir em duas situações.
(Caso 1) 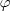
é tal que se i < j temos

.
Como
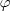
é bijeção entre os naturais, dado M natural existe n* também natural tal que

.
Tomando-se agora n > n*, temos
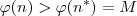
e pela hipótese da convergência de

segue que

.
(Caso 2) 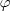
é tal que existem i e j, com i < j, para os quais

.
De modo análogo ao que justificamos antes, dado M natural existe n* também natural tal que

.
Pelo fato de
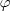
ser bijeção entre os naturais, podemos afirmar que existem
finitos naturais i tais que
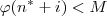
. Seja i* o maior dos naturais que torna essa desigualdade verdadeira. Façamos m = n* + i*.
Para n > m teremos que

, portanto pela hipótese da convergência de

segue que

.
 tal que
tal que  , tenhamos a função
, tenhamos a função uma bijeção. Agora tenhamos uma sequência
uma bijeção. Agora tenhamos uma sequência 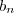 tal que:
tal que:




 ....
.... . (*)
. (*)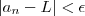 .
.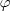 é uma bijeção, temos uma correspondência um a um entre
é uma bijeção, temos uma correspondência um a um entre  e n, para todo n natural. Ou seja que
e n, para todo n natural. Ou seja que  e an tem o mesmo número de termos. Tomando m = M teremos que a partir de n>M a linha (*) acontece, que é o mesmo que
e an tem o mesmo número de termos. Tomando m = M teremos que a partir de n>M a linha (*) acontece, que é o mesmo que  ao invés de
ao invés de 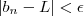 .
.
 . Nesse caso, nem todos os termos a partir de M necessariamente tornam (*) verdadeira.
. Nesse caso, nem todos os termos a partir de M necessariamente tornam (*) verdadeira. .
.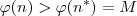 e pela hipótese da convergência de
e pela hipótese da convergência de  .
. .
.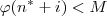 . Seja i* o maior dos naturais que torna essa desigualdade verdadeira. Façamos m = n* + i*.
. Seja i* o maior dos naturais que torna essa desigualdade verdadeira. Façamos m = n* + i*. , portanto pela hipótese da convergência de
, portanto pela hipótese da convergência de 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)