 por maria cleide » Qui Mai 19, 2011 20:08
por maria cleide » Qui Mai 19, 2011 20:08
Se
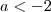
,os valores de x tais que
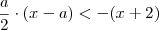
são aqueles que satisfazem:
A-( )
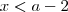
B-( )
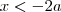
C-( )
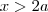
D-( )
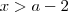
E-( )
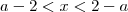
Como desenvolvi:
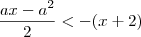


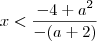
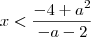
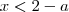
ou
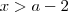
, Meu raciocínio esta correto? Existe outra forma de fazer?
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por MarceloFantini » Qui Mai 19, 2011 20:33
por MarceloFantini » Qui Mai 19, 2011 20:33
Errou na terceira passagem. Se
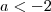
, então
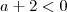
, e portanto dividir a desigualdade por

significa inverter o símbolo. Refaça usando isso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por maria cleide » Sex Ago 26, 2011 23:51
por maria cleide » Sex Ago 26, 2011 23:51
Não entendi, eu só vou inverter o símbolo? Por quê?

vai ficar assim?
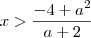
resultado
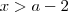
Mas Por quê? Quando eu tenho o x negativo, eu não multiplico toda inequação por -1? Assim invertendo o sinal dos números e o símbolo? Se eu inverter os sinais dos números não encontrarei esta resposta, por isso não entendi o que foi feito.
Obrigada, aguardo ajuda.
Maria Cleide
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INEQUAÇÂO] Inequação do tipo: (a+ x < b + x < c + x)
por Diofanto » Dom Fev 03, 2013 19:55
- 7 Respostas
- 6312 Exibições
- Última mensagem por Diofanto

Qui Fev 14, 2013 23:45
Inequações
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7392 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- Inequação
por Luna » Seg Set 28, 2009 18:55
- 4 Respostas
- 3726 Exibições
- Última mensagem por Molina

Ter Set 29, 2009 16:50
Sistemas de Equações
-
- Inequação
por Luna » Ter Set 29, 2009 16:48
- 1 Respostas
- 2114 Exibições
- Última mensagem por Molina

Qua Set 30, 2009 00:39
Sistemas de Equações
-
- Inequação
por Bebel » Dom Ago 08, 2010 00:50
- 0 Respostas
- 1623 Exibições
- Última mensagem por Bebel

Dom Ago 08, 2010 00:50
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
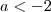 ,os valores de x tais que
,os valores de x tais que 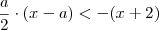 são aqueles que satisfazem:
são aqueles que satisfazem: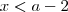
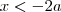
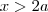
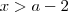
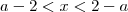
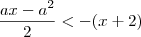


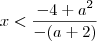
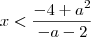
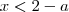 ou
ou 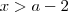 , Meu raciocínio esta correto? Existe outra forma de fazer?
, Meu raciocínio esta correto? Existe outra forma de fazer?
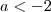 ,os valores de x tais que
,os valores de x tais que 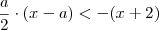 são aqueles que satisfazem:
são aqueles que satisfazem: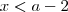
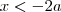
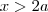
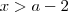
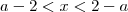
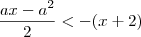


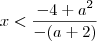
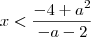
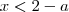 ou
ou 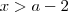 , Meu raciocínio esta correto? Existe outra forma de fazer?
, Meu raciocínio esta correto? Existe outra forma de fazer?
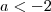 , então
, então 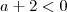 , e portanto dividir a desigualdade por
, e portanto dividir a desigualdade por  significa inverter o símbolo. Refaça usando isso.
significa inverter o símbolo. Refaça usando isso.

 vai ficar assim?
vai ficar assim?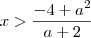 resultado
resultado 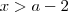

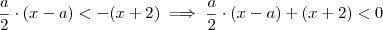
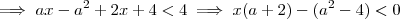
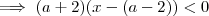
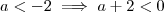 , logo para que este produto seja menor que zero devemos ter
, logo para que este produto seja menor que zero devemos ter 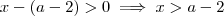 .
.


 .
.



