 por paula luna » Qua Ago 24, 2011 21:38
por paula luna » Qua Ago 24, 2011 21:38
Oi minha resposta nao esta de acordo com o gabarito, alguem pode corrigir minha resoluçao por favor.
Questao:
![\int_{}^{}\frac{{e}^{x}}{\sqrt[2]{{e}^{2x}+1}}dx \int_{}^{}\frac{{e}^{x}}{\sqrt[2]{{e}^{2x}+1}}dx](/latexrender/pictures/eb8ecb7e6a73ad1372098b7fe43de284.png)
Relaçoes:
![\sqrt[2]{{e}^{2x}+1} \sqrt[2]{{e}^{2x}+1}](/latexrender/pictures/0fe446fe70ba900eff470c9c88991e3c.png)


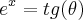
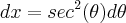
Resoluçao:
![\int_{}^{}\frac{tg(\theta).{sec}^{2}(\theta)}{sec(\theta)}d\theta = \int_{}^{} tg(\theta).sec(\theta)d\theta = sec(\theta) = \sqrt[2]{{e}^{2x}+1} + C \int_{}^{}\frac{tg(\theta).{sec}^{2}(\theta)}{sec(\theta)}d\theta = \int_{}^{} tg(\theta).sec(\theta)d\theta = sec(\theta) = \sqrt[2]{{e}^{2x}+1} + C](/latexrender/pictures/6af88c18465eac64b1864c74f4a1e90e.png)
Resposta certa:
![ln\left| \sqrt[2]{{e}^{2x}+1} + {e}^{x}\right| + C ln\left| \sqrt[2]{{e}^{2x}+1} + {e}^{x}\right| + C](/latexrender/pictures/d84d1e3e794df962d3f3476e16a4ecbc.png)
Bem percebi que no final da resoluçao deveria ter sido
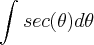
,mas nao sei que parte da minha resoluçao esta errada
-
paula luna
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Mai 05, 2011 21:56
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por paula luna » Qui Ago 25, 2011 00:36
por paula luna » Qui Ago 25, 2011 00:36
Sim, faz sentido pensar nisto à partir da gabarito, no entanto continuo sem entender o porque desta relaçao. Eu estou usando Stewart pra estudar e la ele explica, segundo o que eu entendi, que em uma questao (destas sobre subst. trigon.) deve-se proceder assim:
Caso seja
![\sqrt[]{{x}^{2}+{a}^{2}} \sqrt[]{{x}^{2}+{a}^{2}}](/latexrender/pictures/d1a467a66c503c2714b9447fab557327.png)
( onde o ''x'' representa a variavel da questao e "a" uma constante ):
-
![\sqrt[]{{x}^{2}+{a}^{2}} \sqrt[]{{x}^{2}+{a}^{2}}](/latexrender/pictures/d1a467a66c503c2714b9447fab557327.png)

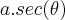
-

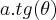
-
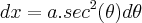
(tem outros dois casos, mas nao ha necessidade de botar aqui)
Bem foi o que eu fiz na questao. Pode talvez ser por se tratar de exponencial e por isso nao estou sabendo como fazer a subst.
-
paula luna
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Mai 05, 2011 21:56
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qui Ago 25, 2011 08:07
por LuizAquino » Qui Ago 25, 2011 08:07
paula luna escreveu:Sim, faz sentido pensar nisto à partir da gabarito, no entanto continuo sem entender o porque desta relaçao. Eu estou usando Stewart pra estudar e la ele explica, segundo o que eu entendi, que em uma questao (destas sobre subst. trigon.) deve-se proceder assim:
Caso seja
![\sqrt[]{{x}^{2}+{a}^{2}} \sqrt[]{{x}^{2}+{a}^{2}}](/latexrender/pictures/d1a467a66c503c2714b9447fab557327.png)
( onde o ''x'' representa a variavel da questao e "a" uma constante ):
![\sqrt[]{{x}^{2}+{a}^{2}} = a.sec(\theta) \sqrt[]{{x}^{2}+{a}^{2}} = a.sec(\theta)](/latexrender/pictures/1af806c867ea11208d9c50cb0fda418c.png)

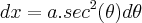
Você não compreendeu como funciona a técnica de substituição. Veja que não estou me referindo a substituição trigonométrica, mas sim a técnica geral de substituição. Eu recomendo que você volte na seção do livro onde explica essa técnica.
Após fazermos
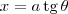
precisamos derivar ambos os membros da equação. Acontece que

. Além disso, temos que

. Colocando agora os termos diferenciais (isto é,

e
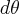
), ficamos com
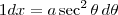
, ou seja,

.
Agora, aplique a mesma ideia considerando que a substituição é

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2840 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2865 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Seg Ago 22, 2011 00:44
- 1 Respostas
- 1427 Exibições
- Última mensagem por LuizAquino

Seg Ago 22, 2011 08:52
Cálculo: Limites, Derivadas e Integrais
-
- Integral Trigonometrica
por Guilherme Carvalho » Dom Abr 01, 2012 22:05
- 2 Respostas
- 1321 Exibições
- Última mensagem por Guilherme Carvalho

Seg Abr 02, 2012 19:29
Cálculo: Limites, Derivadas e Integrais
-
- [Integral trigonométrica]
por vitor_jo » Ter Fev 10, 2015 02:09
- 6 Respostas
- 4525 Exibições
- Última mensagem por Russman

Qua Fev 18, 2015 06:55
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{{e}^{x}}{\sqrt[2]{{e}^{2x}+1}}dx \int_{}^{}\frac{{e}^{x}}{\sqrt[2]{{e}^{2x}+1}}dx](/latexrender/pictures/eb8ecb7e6a73ad1372098b7fe43de284.png)
![\sqrt[2]{{e}^{2x}+1} \sqrt[2]{{e}^{2x}+1}](/latexrender/pictures/0fe446fe70ba900eff470c9c88991e3c.png)


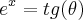
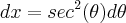
![\int_{}^{}\frac{tg(\theta).{sec}^{2}(\theta)}{sec(\theta)}d\theta = \int_{}^{} tg(\theta).sec(\theta)d\theta = sec(\theta) = \sqrt[2]{{e}^{2x}+1} + C \int_{}^{}\frac{tg(\theta).{sec}^{2}(\theta)}{sec(\theta)}d\theta = \int_{}^{} tg(\theta).sec(\theta)d\theta = sec(\theta) = \sqrt[2]{{e}^{2x}+1} + C](/latexrender/pictures/6af88c18465eac64b1864c74f4a1e90e.png)
![ln\left| \sqrt[2]{{e}^{2x}+1} + {e}^{x}\right| + C ln\left| \sqrt[2]{{e}^{2x}+1} + {e}^{x}\right| + C](/latexrender/pictures/d84d1e3e794df962d3f3476e16a4ecbc.png)
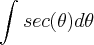 ,mas nao sei que parte da minha resoluçao esta errada
,mas nao sei que parte da minha resoluçao esta errada
![\int_{}^{}\frac{{e}^{x}}{\sqrt[2]{{e}^{2x}+1}}dx \int_{}^{}\frac{{e}^{x}}{\sqrt[2]{{e}^{2x}+1}}dx](/latexrender/pictures/eb8ecb7e6a73ad1372098b7fe43de284.png)
![\sqrt[2]{{e}^{2x}+1} \sqrt[2]{{e}^{2x}+1}](/latexrender/pictures/0fe446fe70ba900eff470c9c88991e3c.png)


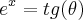
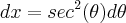
![\int_{}^{}\frac{tg(\theta).{sec}^{2}(\theta)}{sec(\theta)}d\theta = \int_{}^{} tg(\theta).sec(\theta)d\theta = sec(\theta) = \sqrt[2]{{e}^{2x}+1} + C \int_{}^{}\frac{tg(\theta).{sec}^{2}(\theta)}{sec(\theta)}d\theta = \int_{}^{} tg(\theta).sec(\theta)d\theta = sec(\theta) = \sqrt[2]{{e}^{2x}+1} + C](/latexrender/pictures/6af88c18465eac64b1864c74f4a1e90e.png)
![ln\left| \sqrt[2]{{e}^{2x}+1} + {e}^{x}\right| + C ln\left| \sqrt[2]{{e}^{2x}+1} + {e}^{x}\right| + C](/latexrender/pictures/d84d1e3e794df962d3f3476e16a4ecbc.png)
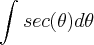 ,mas nao sei que parte da minha resoluçao esta errada
,mas nao sei que parte da minha resoluçao esta errada
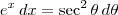

![\sqrt[]{{x}^{2}+{a}^{2}} \sqrt[]{{x}^{2}+{a}^{2}}](/latexrender/pictures/d1a467a66c503c2714b9447fab557327.png) ( onde o ''x'' representa a variavel da questao e "a" uma constante ):
( onde o ''x'' representa a variavel da questao e "a" uma constante ):![\sqrt[]{{x}^{2}+{a}^{2}} \sqrt[]{{x}^{2}+{a}^{2}}](/latexrender/pictures/d1a467a66c503c2714b9447fab557327.png)

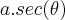

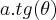
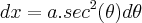

( onde o ''x'' representa a variavel da questao e "a" uma constante ):
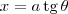 precisamos derivar ambos os membros da equação. Acontece que
precisamos derivar ambos os membros da equação. Acontece que  . Além disso, temos que
. Além disso, temos que  . Colocando agora os termos diferenciais (isto é,
. Colocando agora os termos diferenciais (isto é,  e
e 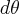 ), ficamos com
), ficamos com 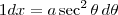 , ou seja,
, ou seja,  .
. .
.