Questao:
![\int_{}^{}\frac{{e}^{x}}{\sqrt[2]{{e}^{2x}+1}}dx \int_{}^{}\frac{{e}^{x}}{\sqrt[2]{{e}^{2x}+1}}dx](/latexrender/pictures/eb8ecb7e6a73ad1372098b7fe43de284.png)
Relaçoes:
![\sqrt[2]{{e}^{2x}+1} \sqrt[2]{{e}^{2x}+1}](/latexrender/pictures/0fe446fe70ba900eff470c9c88991e3c.png)


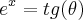
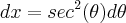
Resoluçao:
![\int_{}^{}\frac{tg(\theta).{sec}^{2}(\theta)}{sec(\theta)}d\theta = \int_{}^{} tg(\theta).sec(\theta)d\theta = sec(\theta) = \sqrt[2]{{e}^{2x}+1} + C \int_{}^{}\frac{tg(\theta).{sec}^{2}(\theta)}{sec(\theta)}d\theta = \int_{}^{} tg(\theta).sec(\theta)d\theta = sec(\theta) = \sqrt[2]{{e}^{2x}+1} + C](/latexrender/pictures/6af88c18465eac64b1864c74f4a1e90e.png)
Resposta certa:
![ln\left| \sqrt[2]{{e}^{2x}+1} + {e}^{x}\right| + C ln\left| \sqrt[2]{{e}^{2x}+1} + {e}^{x}\right| + C](/latexrender/pictures/d84d1e3e794df962d3f3476e16a4ecbc.png)
Bem percebi que no final da resoluçao deveria ter sido
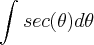 ,mas nao sei que parte da minha resoluçao esta errada
,mas nao sei que parte da minha resoluçao esta errada
![\int_{}^{}\frac{{e}^{x}}{\sqrt[2]{{e}^{2x}+1}}dx \int_{}^{}\frac{{e}^{x}}{\sqrt[2]{{e}^{2x}+1}}dx](/latexrender/pictures/eb8ecb7e6a73ad1372098b7fe43de284.png)
![\sqrt[2]{{e}^{2x}+1} \sqrt[2]{{e}^{2x}+1}](/latexrender/pictures/0fe446fe70ba900eff470c9c88991e3c.png)


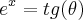
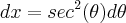
![\int_{}^{}\frac{tg(\theta).{sec}^{2}(\theta)}{sec(\theta)}d\theta = \int_{}^{} tg(\theta).sec(\theta)d\theta = sec(\theta) = \sqrt[2]{{e}^{2x}+1} + C \int_{}^{}\frac{tg(\theta).{sec}^{2}(\theta)}{sec(\theta)}d\theta = \int_{}^{} tg(\theta).sec(\theta)d\theta = sec(\theta) = \sqrt[2]{{e}^{2x}+1} + C](/latexrender/pictures/6af88c18465eac64b1864c74f4a1e90e.png)
![ln\left| \sqrt[2]{{e}^{2x}+1} + {e}^{x}\right| + C ln\left| \sqrt[2]{{e}^{2x}+1} + {e}^{x}\right| + C](/latexrender/pictures/d84d1e3e794df962d3f3476e16a4ecbc.png)
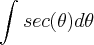 ,mas nao sei que parte da minha resoluçao esta errada
,mas nao sei que parte da minha resoluçao esta errada
paula luna escreveu:mas nao sei que parte da minha resoluçao esta errada
paula luna escreveu:
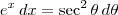

![\sqrt[]{{x}^{2}+{a}^{2}} \sqrt[]{{x}^{2}+{a}^{2}}](/latexrender/pictures/d1a467a66c503c2714b9447fab557327.png) ( onde o ''x'' representa a variavel da questao e "a" uma constante ):
( onde o ''x'' representa a variavel da questao e "a" uma constante ):![\sqrt[]{{x}^{2}+{a}^{2}} \sqrt[]{{x}^{2}+{a}^{2}}](/latexrender/pictures/d1a467a66c503c2714b9447fab557327.png)

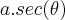

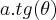
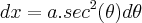

paula luna escreveu:Sim, faz sentido pensar nisto à partir da gabarito, no entanto continuo sem entender o porque desta relaçao. Eu estou usando Stewart pra estudar e la ele explica, segundo o que eu entendi, que em uma questao (destas sobre subst. trigon.) deve-se proceder assim:
Caso seja( onde o ''x'' representa a variavel da questao e "a" uma constante ):
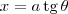 precisamos derivar ambos os membros da equação. Acontece que
precisamos derivar ambos os membros da equação. Acontece que  . Além disso, temos que
. Além disso, temos que  . Colocando agora os termos diferenciais (isto é,
. Colocando agora os termos diferenciais (isto é,  e
e 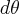 ), ficamos com
), ficamos com 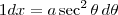 , ou seja,
, ou seja,  .
. .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)