 , sendo g de A a sua inversa. Considere também as seguintes afirmativas. Verifique as falsas e as verdadeiras, justificando sua resposta.
, sendo g de A a sua inversa. Considere também as seguintes afirmativas. Verifique as falsas e as verdadeiras, justificando sua resposta.a) a imagem de f é A.
b) o gráfico de f está acima da reta y = 4
c)
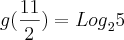
d) Se f (h(x)) = 3 + 2x então h(¼) = 0
e) O gráfico da função g intercepta o eixo x no ponto (1,0)
f) O conjunto solução da inequação
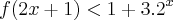 é o intervalo ]0,1[
é o intervalo ]0,1[Se faz necessario as soluções de cada resposta.
A primeira eu fiz e sei que é Falsa pois A não pode ser imagem de f, pois se A é a função então A é o dominio então a imagem será B.

Obrigado, a todos!!!


 , enquanto que sua imagem é
, enquanto que sua imagem é  . Portanto, sua inversa será definida:
. Portanto, sua inversa será definida: 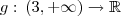 , portanto a primeira é falsa. Seu argumento não é válido pois é possível ter uma função com domínio e imagem iguais. Vamos encontrar a função inversa:
, portanto a primeira é falsa. Seu argumento não é válido pois é possível ter uma função com domínio e imagem iguais. Vamos encontrar a função inversa: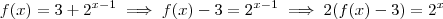

 , temos
, temos 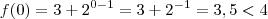 e portanto o gráfico de f não está acima da reta y=4 (existem outros pontos, foi para ilustrar, mesmo porque o conjunto imagem demonstra que há infinitos pontos abaixo da reta).
e portanto o gráfico de f não está acima da reta y=4 (existem outros pontos, foi para ilustrar, mesmo porque o conjunto imagem demonstra que há infinitos pontos abaixo da reta).

 não é contra-exemplo, uma vez que
não é contra-exemplo, uma vez que 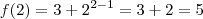 e está acima da reta
e está acima da reta  . Mesmo tomando
. Mesmo tomando  , o seu exemplo não garante que existam pontos do gráfico abaixo da reta.
, o seu exemplo não garante que existam pontos do gráfico abaixo da reta. e ver se o valor é igual ao afirmado na letra C?
e ver se o valor é igual ao afirmado na letra C?