-um fabricante de camisetas que pretendia vender seu estoque no prazo de 4 meses, mantendo o preço de cada camiseta, obteve o seguinte resultado:
- no primeiro mês, vendeu 10% do seu estoque;
- no segundo mês, 20% do restante das mercadorias; e
- no terceiro mês, 50% do que sobrou.
Ao ver que sobraram 3600 camisetas, no quarto mês, o fabricante reduziu o preço de cada um em
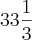 %, conseguindo assim liquidar todo o seu estoque e recebendo R$21600,00 pelas vendas deste mês. É correto afirmar que o fabricante.
%, conseguindo assim liquidar todo o seu estoque e recebendo R$21600,00 pelas vendas deste mês. É correto afirmar que o fabricante.A) Arrecadaria a mesma importancia total, durante os 4 meses, se cada camiseta fosse vendida por x reais, x
![x\in\left[7,8 \right] x\in\left[7,8 \right]](/latexrender/pictures/0bec02c4026cee6aafd3734a0c001538.png) . NO 1ºMÊS VENDERIA ACIMA DE R$12000,00
. NO 1ºMÊS VENDERIA ACIMA DE R$12000,00B) Tinha um estoque que superava 834 duzias de camisetas. 834X12=10008 O ESTOQUE É DE 18000
C) No terceiro mês vendeu uma quantidade de camisetas 200% que no segundo mês. VENDEU 150%
D) No primeiro mês, recebeu mais de R$9000,00. RECEBEU R$16200,00
MINHA RESOLUÇÃO
1º Mês, C(CAMISA) - 0,1C; 0,1C=1800
2º Mês, 0,9C - 0,2C; 0,2C=3600
3º Mês, 0,7C - 0,5C; 0,5C=9000
4º Mês, 0,2C=3600 0,2C=3600
C=3600/0,2=18000 C=18000
VALOR TOTAL(VT)=QUANTIDADE DE CAMISETA(QC) X VALOR UNITÁRIO(VU) - DESCONTO(33,33%)
21600=3600 X 0,66VU
6=0,66VU
VU=R$9,01
Onde foi que errei, se no gabarito do exercício a resposta é o item "A".


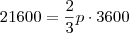

 reais
reais
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.