
Sejam f e g funções definidas por
 e
e 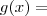 X² + 2 , determine o valor de:
X² + 2 , determine o valor de:![f\left[g\left(\frac {1}{2} \right) \right]+g \left[f(\sqrt5 + 1) \right] f\left[g\left(\frac {1}{2} \right) \right]+g \left[f(\sqrt5 + 1) \right]](/latexrender/pictures/d5c8c5409d3eb58156166e55ef89e7eb.png)
Essa eu tentei e nao consegui, fico grato por uma resposta explicativa.


 e
e 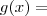 X² + 2 , determine o valor de:
X² + 2 , determine o valor de:![f\left[g\left(\frac {1}{2} \right) \right]+g \left[f(\sqrt5 + 1) \right] f\left[g\left(\frac {1}{2} \right) \right]+g \left[f(\sqrt5 + 1) \right]](/latexrender/pictures/d5c8c5409d3eb58156166e55ef89e7eb.png)

 .
. .
. .
. .
. .
. .
. .
. .
.![f\left[g\left(\frac {1}{2} \right) \right] + g \left[f(\sqrt5 + 1) \right] \Rightarrow \beta + \theta f\left[g\left(\frac {1}{2} \right) \right] + g \left[f(\sqrt5 + 1) \right] \Rightarrow \beta + \theta](/latexrender/pictures/ca6f2673097585bd497f20c111110331.png)


 , confira ai pra mim por favor!
, confira ai pra mim por favor!![f\left[g \left(\frac{1}{2} \right) \right] + f\left[g \left(\frac{1}{2} \right) \right] +](/latexrender/pictures/d31e237c7832a14db9cda2ed658bd04d.png)
![g\left[f(\sqrt5 + 1 \right] g\left[f(\sqrt5 + 1 \right]](/latexrender/pictures/fd316864c9725930f22131e72781bd73.png)

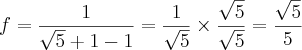






Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.