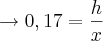 UM observador está em um ponto A do aterro do Flamengo e vê o Pão
UM observador está em um ponto A do aterro do Flamengo e vê o Pãode Açucar segundo um angulo de 10 Graus com o plano horizontal (medido pelo teodolito).
Elenanda em direção ao seu objetivo até um ponto B dinstante 650 m de A e agora vê
o Pão de Açucar segundo um angulo de 14 Graus. Qual a altura
do Pão de Açúcar em relação ao plano de observação?
Fiz dessa forma:


Temos:

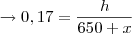
Da primeira equação temos:
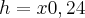
Introduzindo a primeira equação na segunda temos:

Mas a resposta correta é 391,40 m Bom! ja sabe o que fazer!
Olha ai e encontre meu erro por favor!
Obrigado!!


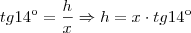

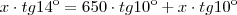

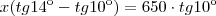
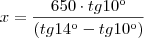

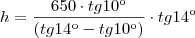



 .
.
 :
: