 por killerkill » Sex Ago 12, 2011 23:10
por killerkill » Sex Ago 12, 2011 23:10
Olá pessoal, é o seguinte, chega mais um final de semana. Mais 2 dias "free" pra estudar.
Mais a minha dúvida é a seguinte. Tem a seguinte questão:
Explique porque a função é descontínua num dado numero a, e esboce o gráfico:
a=3

se

e

se
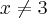
Vou explicar minha resolução:
Sendo a continuidade a ser analizada no valor a=3, é possível afirmar que f(3)=6.
e
Quando
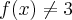

então,

Portanto, o limite de tal função não é contínuo em a=3, pois
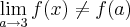
Até aí eu acho que fiz tudo certo, só que para eu esboçar o gráfico é que tenho certa dúvida. Não sei desenhar o gráfico aqui no Fórum, demorei mais de 30 minutos pra escrever isso daí com o editor de fórmulas, imagine o gráfico. mais é o seguinte: imagine x vindo pela esquerda e pela direita ... f(x)=7. só que eu não sei como desenhar essa curva vindo da direita ou pela esquerda. porque a função limite nesse ponto é muito complicada para min desenhar esse tipo de gráfico. Digo, eu não sei se a curva vem se cima.. ou se baixo.. etc. eu sei só desenhar graficos de 2 grau, exponencial etc... mais um gráfico do tipo:

eu não tenho a mínima ideia.
A propósito, essa será minha primeira prova de Calculo aqui na federal do meu estado. Tenho certas dúvidas, queria uma opinião de vocês que são mais experientes. Se eu explicar exatamente dessa forma seria o mais ideal ou não? eu deveria apenas deixar o calculo puro e frio e pronto?
Valew pela atenção e bom final de semana pra todos
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Sex Ago 12, 2011 23:33
por LuizAquino » Sex Ago 12, 2011 23:33
O exercício fornece a função:
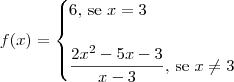
Para saber se f é contínua em 3, precisamos verificar se
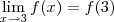
.
Pois bem, calculando o limite:


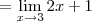

Por outro lado, sabemos que f(3) = 6. Concluímos que

e portanto f não é contínua em 3.
Para esboçar o gráfico, basta perceber que essa função pode ser reescrita como:
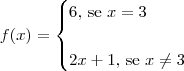 Observações
Observaçõeskillerkill escreveu:Não sei desenhar o gráfico aqui no Fórum
Use um programa específico, como por exemplo o
GeoGebra. Depois é só anexar o arquivo de imagem na sua mensagem. Se deseja um tutorial de como usar esse programa, então eu gostaria de recomendar que visite meu canal:
http://www.youtube.com/LCMAquinokillerkill escreveu:A propósito, essa será minha primeira prova de Calculo aqui na federal do meu estado. Tenho certas dúvidas, queria uma opinião de vocês que são mais experientes. Se eu explicar exatamente dessa forma seria o mais ideal ou não?
Em verdade, veja que a sua solução está desorganizada. Muito provavelmente você perderia pontos devido a isso.
Por exemplo, perceba que você escreveu o símbolo de limite apenas uma vez e em seguida fez todo o desenvolvimento sem usá-lo. Isso está incorreto. Veja na resolução acima que o símbolo de limite apenas desaparece no final da resolução.
Além disso, você colocou sem necessidade a expressão

no limite, quando poderia apenas escrever
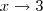
.
killerkill escreveu:eu deveria apenas deixar o calculo puro e frio e pronto?
Isso depende do professor. O ideal é você perguntar a ele antes da avaliação.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por killerkill » Sex Ago 12, 2011 23:59
por killerkill » Sex Ago 12, 2011 23:59
Estou com dificuldades no gráfico, nao consigo postar aqui.. Extençao GGB nao permitida
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Sáb Ago 13, 2011 00:02
por LuizAquino » Sáb Ago 13, 2011 00:02
killerkill escreveu:Estou com dificuldades no gráfico, nao consigo postar aqui.. Extençao GGB nao permitida
Após fazer o desenho, use o menu "Arquivo > Exportar > Janela de Visualização como Figura (png, eps)".
Uma dica: redimensione a janela do programa antes de exportar. Caso contrário a sua imagem pode ficar muito grande.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por killerkill » Sáb Ago 13, 2011 00:06
por killerkill » Sáb Ago 13, 2011 00:06
ops, Agora eu entendi, ela vai ser uma reta com raíz -1/2 e f(0)=1... nunca imaginaria que seria uma reta... mais agora eu entendi. é uma RETA que em f(3)=6 deixando uma "bolinha aberta na reta) uma ves que ela esta definida em outro local da reta.. entendi! obrigado pela ajuda... e pela dica tambem.. realmente o modo como voce explicou é bem mais eficiente e claro. obrigado
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6647 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [gráfico de função] Dúvida em questões do CESPE
por rogerioandre » Qua Jun 06, 2012 19:07
- 1 Respostas
- 1359 Exibições
- Última mensagem por Russman

Qua Jun 06, 2012 23:26
Funções
-
- [limite] Dúvida limite com raizes
por rqaugusto » Dom Abr 30, 2017 23:23
- 0 Respostas
- 3119 Exibições
- Última mensagem por rqaugusto

Dom Abr 30, 2017 23:23
Cálculo: Limites, Derivadas e Integrais
-
- Limite - Duvida
por Claudin » Qua Mai 18, 2011 18:32
- 3 Respostas
- 2601 Exibições
- Última mensagem por Claudin

Qua Mai 18, 2011 20:45
Cálculo: Limites, Derivadas e Integrais
-
- Duvida - Limite
por Claudin » Qua Mai 18, 2011 21:19
- 6 Respostas
- 3312 Exibições
- Última mensagem por Claudin

Qui Mai 19, 2011 12:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 se
se 

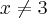
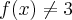


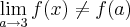




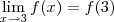 .
.

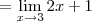

 e portanto f não é contínua em 3.
e portanto f não é contínua em 3.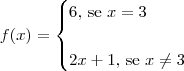
 no limite, quando poderia apenas escrever
no limite, quando poderia apenas escrever 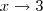 .
.
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: