Mais a minha dúvida é a seguinte. Tem a seguinte questão:
Explique porque a função é descontínua num dado numero a, e esboce o gráfico:
a=3
 se
se 
e

se
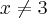
Vou explicar minha resolução:
Sendo a continuidade a ser analizada no valor a=3, é possível afirmar que f(3)=6.
e
Quando
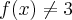

então,

Portanto, o limite de tal função não é contínuo em a=3, pois
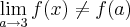
Até aí eu acho que fiz tudo certo, só que para eu esboçar o gráfico é que tenho certa dúvida. Não sei desenhar o gráfico aqui no Fórum, demorei mais de 30 minutos pra escrever isso daí com o editor de fórmulas, imagine o gráfico. mais é o seguinte: imagine x vindo pela esquerda e pela direita ... f(x)=7. só que eu não sei como desenhar essa curva vindo da direita ou pela esquerda. porque a função limite nesse ponto é muito complicada para min desenhar esse tipo de gráfico. Digo, eu não sei se a curva vem se cima.. ou se baixo.. etc. eu sei só desenhar graficos de 2 grau, exponencial etc... mais um gráfico do tipo:

eu não tenho a mínima ideia.
A propósito, essa será minha primeira prova de Calculo aqui na federal do meu estado. Tenho certas dúvidas, queria uma opinião de vocês que são mais experientes. Se eu explicar exatamente dessa forma seria o mais ideal ou não? eu deveria apenas deixar o calculo puro e frio e pronto?
Valew pela atenção e bom final de semana pra todos


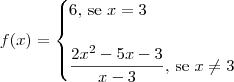
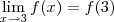 .
.

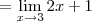

 e portanto f não é contínua em 3.
e portanto f não é contínua em 3.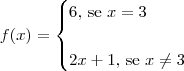
 no limite, quando poderia apenas escrever
no limite, quando poderia apenas escrever 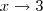 .
.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.