Calculo percentual não da valor exato?

por **fabianosilva** » Qua Ago 10, 2011 17:07

[Calculo percentual não da valor exato?]

Tenho o seguinte cenário.

Tenho um valor total = 1000, sendo que deste valor estou usando 80% = 800 e tenho 20% = 200 livre.

Portanto preciso calcular o valor para obter 25% de àrea livre.

Minhas tentativas.

1000+ (1000 *25/100) = 1250 --> (1250*25/100) = 312,5.
Como eu adicionei 250 e fiquei com 1250, logo tenho os 250 livres mais os 200 que ja tinha que é igual = 450 que representa mais que 25%

Gostaria de ter 25% livre, qual o valor que eu preciso adicionar para eu obter os 25% livre, sendo que eu tenho hoje 20% livre.

Qual o calculo exato para isso?

Obrigado
Fabiano

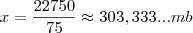
por **Molina** » Qua Ago 10, 2011 20:31

Boa noite, Fabiano.

Coloque o enunciado da questão na íntegra, para facilitar o entendimento do que você quer.

Fico no aguardo.

por **fabianosilva** » Qui Ago 11, 2011 16:11

Ok,

Vou descrever a situação real que tenho. para tentar melhorar onde realmente estou querendo chegar.

Tenho um disco rigido no meu computar com 1000 gb total estou usando 910 megas tenho disponivel 90megas. Portanto tenho 9% livre e gostaria de deixa-lo com 25% livre mas não posso apagar minhas informações. então preciso aumentar meu disco em x% para que eu fique com 25% livre.

Minhas tentativas (1000*25)/100 = 250. Se eu somar os 250 + 1000 ficarei com 1250gigas total e 25% disso será 312,5 só que terei disponível 250+90=340 =27,2%.

Ficarei com 27.2% e não os meus 25 que gostaria.

Obrigado pela ajuda.

Fabiano Silva

por **Molina** » Qui Ago 11, 2011 16:35

Boa tarde, Fabiano.

Agora ficou mais claro. O que você quer é aumentar seu HD de modo que fique com 25% livre e 75% ocupado.

Uma regra de três simples e o problema está resolvido, veja:

910mb - 75% (espaço ocupado)
x mb - 25% (espaço livre)

Multiplique cruzado estes valores. Você deve encontrar $x = \frac{22750}{75} \approx 303,333... mb$

Esse é o espaço livre que você quer. Some-o com o espaço ocupado e subtraia 1gb desse valor.

Qualquer dúvida, informe! :y:

por **fabianosilva** » Qui Ago 11, 2011 17:28

Boa tarde Diego,

Cara te agradeço muito. realmente não pensei no espaço usado utlizando a regra de 3.

Estou extremamente embasbacado.

Muitissimo Obrigado.

Fabiano Silva