 por killerkill » Ter Ago 09, 2011 23:12
por killerkill » Ter Ago 09, 2011 23:12
é o seguinte.. Tenho uma questão aqui do livro Cálculo I( James Stewart)

aplicando os principios de módulo aí (até onde eu sei) fica duas possibilidades...
1.
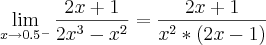
2.
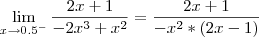
Daí pra frente não consigo fazer mais nada já que não consigo eliminar termos nessas equações...
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Qua Ago 10, 2011 09:55
por LuizAquino » Qua Ago 10, 2011 09:55
Perceba que nesse limite não há uma indeterminação.
O numerador tende para 2 enquanto que o denominador tende para 0 (e sempre será positivo não importando o lado que x se aproxima de 0,5).
Desse modo, temos que:

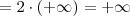
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por killerkill » Qua Ago 10, 2011 10:29
por killerkill » Qua Ago 10, 2011 10:29
Pois é, mais no gabarito do livro a resposta é -1/2
=/
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Qua Ago 10, 2011 10:33
por LuizAquino » Qua Ago 10, 2011 10:33
killerkill escreveu:Pois é, mais no gabarito do livro a resposta é -1/2
=/
Se o limite é exatamente esse que você escreveu, então o gabarito fornecido no livro está errado.
Em que seção está esse exercício e qual é a edição do livro de Stewart que você está usando?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por killerkill » Qua Ago 10, 2011 10:46
por killerkill » Qua Ago 10, 2011 10:46
Livro do Stewart só que o sexta ediçao ( o ultimo lançado) Volume 1 - Exercicios 2.3 questao 29 - pagina 96
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Qua Ago 10, 2011 11:10
por LuizAquino » Qua Ago 10, 2011 11:10
killerkill escreveu:Livro do Stewart só que o sexta ediçao ( o ultimo lançado) Volume 1 - Exercicios 2.3 questao 29 - pagina 96
No momento eu estou com a 5ª edição e nessa seção não há esse exercício.
De qualquer modo, o correto é como indiquei acima:
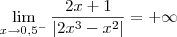
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por killerkill » Qua Ago 10, 2011 11:38
por killerkill » Qua Ago 10, 2011 11:38
Luiz, eu fiz uma confusão louca aqui. Mil desculpas. A questão é que eu olhei no livro desde o começo erroneamente. Primeiro erro meu: a questão é na verdade a seguinte:
Alem disso.. eu olhei o gabarito errado, o exercício é o 41 e não 29. Ou seja, eu Errei foi tudo!
de fato essa questão é super fácil quando se está certa!
e no gabarito a resposta é -4
Desculpe pelo encômodo, esses dias tem sido de grande exaustão resolvendo os exercícios. nunca estudei tanto.
Muito obrigado pela atenção, e desculpas novamente.
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Qua Ago 10, 2011 11:47
por LuizAquino » Qua Ago 10, 2011 11:47
De fato, se o exercício é na verdade
, então o resultado é -4.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- limite envolvendo modulo
por matmatco » Qui Mar 22, 2012 23:18
- 7 Respostas
- 4621 Exibições
- Última mensagem por LuizAquino

Ter Mar 27, 2012 13:14
Cálculo: Limites, Derivadas e Integrais
-
- [integral envolvendo módulo]
por Fabio Wanderley » Sex Dez 14, 2012 11:14
- 3 Respostas
- 2700 Exibições
- Última mensagem por young_jedi

Sex Dez 14, 2012 16:04
Cálculo: Limites, Derivadas e Integrais
-
- Limite com Módulo
por Man Utd » Sex Mai 10, 2013 10:45
- 6 Respostas
- 8891 Exibições
- Última mensagem por Man Utd

Sáb Mai 11, 2013 14:29
Cálculo: Limites, Derivadas e Integrais
-
- Limite com Modulo em denominador
por orainha » Sex Fev 03, 2017 23:12
- 2 Respostas
- 8292 Exibições
- Última mensagem por orainha

Qui Mar 30, 2017 21:42
Cálculo: Limites, Derivadas e Integrais
-
- limite envolvendo exponencial
por renat » Dom Jun 11, 2017 20:37
- 0 Respostas
- 2835 Exibições
- Última mensagem por renat

Dom Jun 11, 2017 20:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



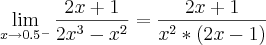
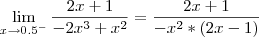


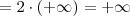




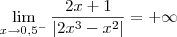

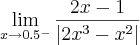

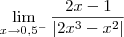 , então o resultado é -4.
, então o resultado é -4.


 , avisa que eu resolvo.
, avisa que eu resolvo.

