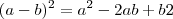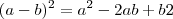por LuizCarlos » Qui Ago 04, 2011 11:23
por LuizCarlos » Qui Ago 04, 2011 11:23
Não estou entendendo a representação geométrica, do quadrado da diferença de dois termos!
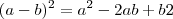
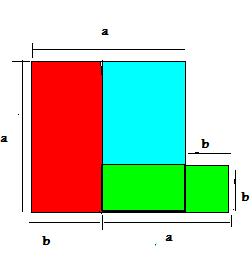
Como seria nesse desenho que postei? seria, a área do quadrado maior - a área do retangulo vermelho - a área do retangulo verde?
Restando o quadrado azul e o quadrado verde?
Não estou entendendo.
- Anexos
-
- diferencaa.JPG (6.8 KiB) Exibido 2167 vezes
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Caradoc » Sex Ago 19, 2011 09:34
por Caradoc » Sex Ago 19, 2011 09:34
(a-b)² representa a área do quadrado azul.
Que é a mesma área se fizermos o quadrado grande - o retângulo vermelho - o retângulo verde ( note que o ao subtrair o retângulo verde, tiramos também o quadradinho b² que não está contido no quadrado grande), + o quadradinho verde, que é para compensar termos tirado ele antes. Restando denovo apenas o quadrado azul.
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Representação Geométrica do quadrado da diferença
 por LuizCarlos » Qui Ago 04, 2011 02:42
por LuizCarlos » Qui Ago 04, 2011 02:42
- 3 Respostas
- 6106 Exibições
- Última mensagem por Marcelo RoX

Dom Jun 30, 2013 23:24
Álgebra Elementar
-
- [Vetores]Representação Geométrica
por IlgssonBraga » Sex Jul 19, 2013 16:18
- 2 Respostas
- 2451 Exibições
- Última mensagem por IlgssonBraga

Sáb Jul 20, 2013 18:55
Geometria Analítica
-
- [Números Complexos] Representação geométrica
por mota_16 » Sáb Dez 28, 2013 23:10
- 5 Respostas
- 5516 Exibições
- Última mensagem por e8group

Seg Dez 30, 2013 21:07
Números Complexos
-
- Fatoração e diferença de quadrado e cubo.
por torilleon » Sex Ago 19, 2011 20:27
- 5 Respostas
- 2685 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 20, 2011 14:21
Álgebra Elementar
-
- Trinomio Quadrado Perfeito (Complemento de quadrado)
por IgorFilipe » Qua Ago 17, 2011 23:01
- 2 Respostas
- 3750 Exibições
- Última mensagem por IgorFilipe

Qui Ago 18, 2011 15:52
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.