Temos a equação:
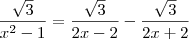
Note que x não pode ser 1 e nem -1, pois caso contrário ocorreria divisões por zero.
Podemos reescrever essa equação como:

Dividindo toda essa equação por

, ficamos com:

Agora, multiplicando toda essa equação por
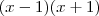
, ficamos com:
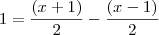
A partir daí tente terminar de resolver o exercício.
ObservaçãoJoan escreveu:obs: esse "Â" no primeiro termo nao existe nem sei pq saiu...
Isso apareceu pois no ambiente LaTeX você usou o atalho do teclado para escrever o símbolo "²". O correto é usar o seguinte comando:
- Código: Selecionar todos
[tex]x^2[/tex]
O resultado desse comando é:

.
![\frac{\sqrt[]{3}}{x²-1} = \frac{\sqrt[]{3}}{2x-2} - \frac{\sqrt[]{3}}{2x+2} ? \frac{\sqrt[]{3}}{x²-1} = \frac{\sqrt[]{3}}{2x-2} - \frac{\sqrt[]{3}}{2x+2} ?](/latexrender/pictures/3d7ba65e61b507b72abd4a870ec072d4.png)
![\frac{\sqrt[]{3}}{(x-1)(x+1)} = \frac{\sqrt[]{3}}{2(x-1)} - \frac{\sqrt[]{3}}{2(x+1)} \frac{\sqrt[]{3}}{(x-1)(x+1)} = \frac{\sqrt[]{3}}{2(x-1)} - \frac{\sqrt[]{3}}{2(x+1)}](/latexrender/pictures/2fe44ab138897da03562555542037d99.png)


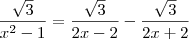

 , ficamos com:
, ficamos com:
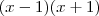 , ficamos com:
, ficamos com: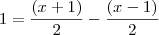
 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)