 por Joan » Sáb Jul 23, 2011 12:06
por Joan » Sáb Jul 23, 2011 12:06

No conjunto R dos numeros reais, qual será o conjunto solução da equação:
![\frac{\sqrt[]{3}}{x²-1} = \frac{\sqrt[]{3}}{2x-2} - \frac{\sqrt[]{3}}{2x+2} ? \frac{\sqrt[]{3}}{x²-1} = \frac{\sqrt[]{3}}{2x-2} - \frac{\sqrt[]{3}}{2x+2} ?](/latexrender/pictures/3d7ba65e61b507b72abd4a870ec072d4.png)
Ai eu fui resolvendo da seguinte maneira:
![\frac{\sqrt[]{3}}{(x-1)(x+1)} = \frac{\sqrt[]{3}}{2(x-1)} - \frac{\sqrt[]{3}}{2(x+1)} \frac{\sqrt[]{3}}{(x-1)(x+1)} = \frac{\sqrt[]{3}}{2(x-1)} - \frac{\sqrt[]{3}}{2(x+1)}](/latexrender/pictures/2fe44ab138897da03562555542037d99.png)
Tendo o MMC = 2(x+1)(x-1), peguei dividi pelo denominador, e fui multiplicar pelos numeradores que são raizes de três, e eu nao sei como fazer de agora em diante....
desde já grato....
obs: esse "Â" no primeiro termo nao existe nem sei pq saiu...
-
Joan
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Jul 22, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Sáb Jul 23, 2011 13:03
por LuizAquino » Sáb Jul 23, 2011 13:03
Temos a equação:
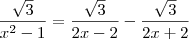
Note que x não pode ser 1 e nem -1, pois caso contrário ocorreria divisões por zero.
Podemos reescrever essa equação como:

Dividindo toda essa equação por

, ficamos com:

Agora, multiplicando toda essa equação por
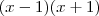
, ficamos com:
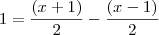
A partir daí tente terminar de resolver o exercício.
ObservaçãoJoan escreveu:obs: esse "Â" no primeiro termo nao existe nem sei pq saiu...
Isso apareceu pois no ambiente LaTeX você usou o atalho do teclado para escrever o símbolo "²". O correto é usar o seguinte comando:
- Código: Selecionar todos
[tex]x^2[/tex]
O resultado desse comando é:

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Joan » Sáb Jul 23, 2011 13:21
por Joan » Sáb Jul 23, 2011 13:21
Obrigado vou tentar resolver aki... vlw mesmo...
Consegui, obrigado, muito obrigado...
-
Joan
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Jul 22, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [triângulo equilátero] Questão Colégio Naval 2010
 por Joan » Sex Jul 22, 2011 18:42
por Joan » Sex Jul 22, 2011 18:42
- 3 Respostas
- 3722 Exibições
- Última mensagem por Joan

Sáb Jul 23, 2011 11:34
Geometria Plana
-
- MMC e MDC - Colégio Naval
por igorcamilo » Sáb Jun 25, 2011 21:22
- 1 Respostas
- 2031 Exibições
- Última mensagem por FilipeCaceres

Dom Jun 26, 2011 16:13
Álgebra Elementar
-
- Colégio Naval
por Joan » Seg Jul 25, 2011 16:38
- 8 Respostas
- 8327 Exibições
- Última mensagem por LuizAquino

Ter Jul 26, 2011 21:35
Álgebra Elementar
-
- Divisibilidade - Colégio naval
por igorcamilo » Sex Jun 24, 2011 19:22
- 2 Respostas
- 2461 Exibições
- Última mensagem por igorcamilo

Sex Jun 24, 2011 20:32
Álgebra Elementar
-
- Colégio Naval - Aritmética dos inteiros
por eliky » Sex Mai 17, 2013 01:16
- 1 Respostas
- 2333 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 20:40
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\sqrt[]{3}}{x²-1} = \frac{\sqrt[]{3}}{2x-2} - \frac{\sqrt[]{3}}{2x+2} ? \frac{\sqrt[]{3}}{x²-1} = \frac{\sqrt[]{3}}{2x-2} - \frac{\sqrt[]{3}}{2x+2} ?](/latexrender/pictures/3d7ba65e61b507b72abd4a870ec072d4.png)
![\frac{\sqrt[]{3}}{(x-1)(x+1)} = \frac{\sqrt[]{3}}{2(x-1)} - \frac{\sqrt[]{3}}{2(x+1)} \frac{\sqrt[]{3}}{(x-1)(x+1)} = \frac{\sqrt[]{3}}{2(x-1)} - \frac{\sqrt[]{3}}{2(x+1)}](/latexrender/pictures/2fe44ab138897da03562555542037d99.png)


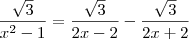

 , ficamos com:
, ficamos com:
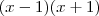 , ficamos com:
, ficamos com: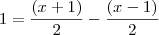
 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.