CONCURSO PETROBRAS 2011:
O grafico abaixo mostra,parcialmente, o grafico da funcao f(x), definida por f(x)= (3x^2)/ (x³+1)
Qual o valor da area limitada pela curva do grafico f, pelo eixo das abscissas e pelas retas x=1 e x=3?
PS. A figura do grafico mostra que a funcao f(x) é positiva no intervalo [1,3].
Gabarito: ln(14)


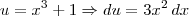 , e portanto a integral será
, e portanto a integral será  , basta colocar os limites de integração. Note que quando fazemos mudança de variável é necessário alterar os limites para que o valor final não se altere.
, basta colocar os limites de integração. Note que quando fazemos mudança de variável é necessário alterar os limites para que o valor final não se altere.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)