 por Claudin » Sex Jul 01, 2011 03:45
por Claudin » Sex Jul 01, 2011 03:45
Fazendo exercícios do livro de Guidorizzi
Deparei com tal dúvida:
![\lim_{x\rightarrow1}\frac{\sqrt[]{x}-1}{\sqrt[]{2x+3}-\sqrt[]{5}} \lim_{x\rightarrow1}\frac{\sqrt[]{x}-1}{\sqrt[]{2x+3}-\sqrt[]{5}}](/latexrender/pictures/dd7842e72b270906fddd527b94344be1.png) OBS: Sem utilizar L'Hopital
OBS: Sem utilizar L'Hopital"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Sex Jul 01, 2011 03:47
por Claudin » Sex Jul 01, 2011 03:47
Não consegui desenvolver corretamente por isso não postei nada, espero que alguém mostre uma solução plausível. Obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Ter Jul 05, 2011 15:35
por Claudin » Ter Jul 05, 2011 15:35
Mas multiplicando por
![\sqrt[]{x}+1 \sqrt[]{x}+1](/latexrender/pictures/e2db15bd6cfb24507921c2cf2f90dd2b.png)
não chegaria no resultado não?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Ter Jul 05, 2011 17:49
por LuizAquino » Ter Jul 05, 2011 17:49
Claudin escreveu:Mas multiplicando por
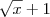
não chegaria no resultado não?
Não.
Ainda que você multiplica-se apenas por essa expressão e fizesse as devidas simplificações, em seguida você iria precisar multiplicar por
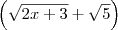
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qua Jul 20, 2011 15:18
por Claudin » Qua Jul 20, 2011 15:18
Mesmo utilizando a multiplicação fornecida pelo Luiz Aquino, não obtive o resultado correto, mas, acho que encontrei meu erro.
Quando multiplica-se
![{\sqrt[]{2x+3}-\sqrt[]{5}).(\sqrt[]{2x+3}+\sqrt[]{5}) {\sqrt[]{2x+3}-\sqrt[]{5}).(\sqrt[]{2x+3}+\sqrt[]{5})](/latexrender/pictures/eae814cf831bd42a2ec6a65294e5b9c2.png)
e quando multiplica-se
![\sqrt[]{x}-1.\sqrt[]{x}+1 \sqrt[]{x}-1.\sqrt[]{x}+1](/latexrender/pictures/0a261323031b61919d4b9e44febb5c45.png)
Qual resultado é obtido?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Qua Jul 20, 2011 15:44
por Claudin » Qua Jul 20, 2011 15:44
Só não compreendi uma coisa
Sendo:
![x-1=(\sqrt[]{x}+1).(\sqrt[]{x}-1) x-1=(\sqrt[]{x}+1).(\sqrt[]{x}-1)](/latexrender/pictures/ca9deaabaf81bcedb51de1e9a71cfd95.png)
correto?
Na hora de fazer as devidas simplificações resultou em
![2(\sqrt[]{x}+1) 2(\sqrt[]{x}+1)](/latexrender/pictures/7848b0a82a0e67a3eb60e407a434f2e4.png)
Ou seja, você simplificou
![(\sqrt[]{x}+1) (\sqrt[]{x}+1)](/latexrender/pictures/3cbcc88d07f3f578a5108370b3ab5c41.png)
com
![(\sqrt[]{x}-1) (\sqrt[]{x}-1)](/latexrender/pictures/8cf1007420f452c8ac99a4718e6b92ce.png)
correto?
Porque não poderia ter simplificado
![(\sqrt[]{x}+1) (\sqrt[]{x}+1)](/latexrender/pictures/3cbcc88d07f3f578a5108370b3ab5c41.png)
com
![(\sqrt[]{x}-1) (\sqrt[]{x}-1)](/latexrender/pictures/8cf1007420f452c8ac99a4718e6b92ce.png)
ai resultaria em uma indeterminação.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Jul 20, 2011 16:12
por LuizAquino » Qua Jul 20, 2011 16:12
Claudin escreveu:Sendo:
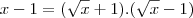
correto?
Sim, está correto.
Claudin escreveu:Na hora de fazer as devidas simplificações resultou em
![2(\sqrt[]{x}+1) 2(\sqrt[]{x}+1)](/latexrender/pictures/7848b0a82a0e67a3eb60e407a434f2e4.png)
Ou seja, você simplificou
![(\sqrt[]{x}+1) (\sqrt[]{x}+1)](/latexrender/pictures/3cbcc88d07f3f578a5108370b3ab5c41.png)
com
![(\sqrt[]{x}-1) (\sqrt[]{x}-1)](/latexrender/pictures/8cf1007420f452c8ac99a4718e6b92ce.png)
correto?
Não está correto. No denominador simplesmente foi usado a propriedade comutativa do produto:
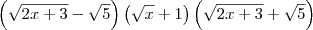
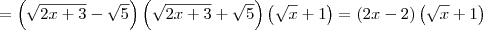
.
Porque não poderia ter simplificado
![(\sqrt[]{x}+1) (\sqrt[]{x}+1)](/latexrender/pictures/3cbcc88d07f3f578a5108370b3ab5c41.png)
com
![(\sqrt[]{x}-1) (\sqrt[]{x}-1)](/latexrender/pictures/8cf1007420f452c8ac99a4718e6b92ce.png)
ai resultaria em uma indeterminação.
A indeterminação desse limite só será retirada quando eliminarmos os fatores (x - 1) que aparecem no numerador e no denominador.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6642 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5117 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7257 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4434 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow1}\frac{\sqrt[]{x}-1}{\sqrt[]{2x+3}-\sqrt[]{5}} \lim_{x\rightarrow1}\frac{\sqrt[]{x}-1}{\sqrt[]{2x+3}-\sqrt[]{5}}](/latexrender/pictures/dd7842e72b270906fddd527b94344be1.png)

![\lim_{x\rightarrow1}\frac{\sqrt[]{x}-1}{\sqrt[]{2x+3}-\sqrt[]{5}} \lim_{x\rightarrow1}\frac{\sqrt[]{x}-1}{\sqrt[]{2x+3}-\sqrt[]{5}}](/latexrender/pictures/dd7842e72b270906fddd527b94344be1.png)


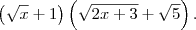

![\sqrt[]{x}+1 \sqrt[]{x}+1](/latexrender/pictures/e2db15bd6cfb24507921c2cf2f90dd2b.png) não chegaria no resultado não?
não chegaria no resultado não?
não chegaria no resultado não?
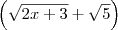 .
.
![{\sqrt[]{2x+3}-\sqrt[]{5}).(\sqrt[]{2x+3}+\sqrt[]{5}) {\sqrt[]{2x+3}-\sqrt[]{5}).(\sqrt[]{2x+3}+\sqrt[]{5})](/latexrender/pictures/eae814cf831bd42a2ec6a65294e5b9c2.png)
![\sqrt[]{x}-1.\sqrt[]{x}+1 \sqrt[]{x}-1.\sqrt[]{x}+1](/latexrender/pictures/0a261323031b61919d4b9e44febb5c45.png)

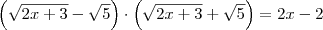
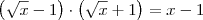
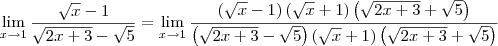
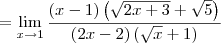
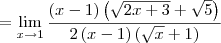
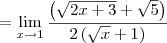
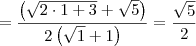

![x-1=(\sqrt[]{x}+1).(\sqrt[]{x}-1) x-1=(\sqrt[]{x}+1).(\sqrt[]{x}-1)](/latexrender/pictures/ca9deaabaf81bcedb51de1e9a71cfd95.png) correto?
correto?![2(\sqrt[]{x}+1) 2(\sqrt[]{x}+1)](/latexrender/pictures/7848b0a82a0e67a3eb60e407a434f2e4.png)
![(\sqrt[]{x}+1) (\sqrt[]{x}+1)](/latexrender/pictures/3cbcc88d07f3f578a5108370b3ab5c41.png) com
com ![(\sqrt[]{x}-1) (\sqrt[]{x}-1)](/latexrender/pictures/8cf1007420f452c8ac99a4718e6b92ce.png) correto?
correto?![(\sqrt[]{x}+1) (\sqrt[]{x}+1)](/latexrender/pictures/3cbcc88d07f3f578a5108370b3ab5c41.png) com
com ![(\sqrt[]{x}-1) (\sqrt[]{x}-1)](/latexrender/pictures/8cf1007420f452c8ac99a4718e6b92ce.png)

correto?
com
correto?
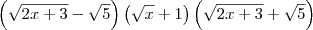
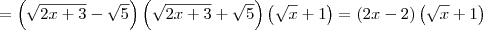 .
.com

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.