 por giulioaltoe » Qua Jul 20, 2011 09:43
por giulioaltoe » Qua Jul 20, 2011 09:43
estou entrando em derivada agora, quando eu possuo uma funçao que pode apresentar divisão de polinomios e me pedem para derivar e necessário,se possivel, simplificar a equação antes?
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por LuizAquino » Qua Jul 20, 2011 09:58
por LuizAquino » Qua Jul 20, 2011 09:58
Não é necessário fazer a simplificação antes, mas isso pode lhe poupar trabalho.
Faça um teste!
Considere as funções
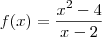
e

. Considere ainda que o domínio delas seja o mesmo:

.
Agora, calcule a derivada dessas funções.
O que aconteceu?
ObservaçãoNa teoria de conjuntos, a notação
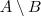
é o mesmo que

.
Atenção!
Não confundir a notação acima com
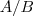
.
SugestãoSe quiser um canal no YouTube com vídeo-aulas sobre derivadas (e demais conceitos do Cálculo), então eu espero que o meu canal possa lhe ajudar:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por giulioaltoe » Qua Jul 20, 2011 10:27
por giulioaltoe » Qua Jul 20, 2011 10:27
consegui entender a idea passada!
mas se eu tiver uma equação mais complexa do tipo

e pede pra achar a derivada?? eu tentei jogar na formula
![\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2} \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}](/latexrender/pictures/895a3c67e97b6b6a64a5af986d1ac5fd.png)
e deu uns numeros muito extenso, é normal e eu tenho que simplificar depois, ou tem algo errado?
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por LuizAquino » Qua Jul 20, 2011 10:47
por LuizAquino » Qua Jul 20, 2011 10:47
Não se assuste se a derivada de uma função ficar "extensa". Algumas são assim mesmo. É o caso dessa última que você postou.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por giulioaltoe » Qua Jul 20, 2011 12:54
por giulioaltoe » Qua Jul 20, 2011 12:54
beleza entao, brigadão!
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada - Um Conceito Teórico
por Fabio Cabral » Ter Jun 07, 2011 10:41
- 5 Respostas
- 2828 Exibições
- Última mensagem por MarceloFantini

Ter Jun 07, 2011 12:45
Cálculo: Limites, Derivadas e Integrais
-
- conceito de integral e limite
por OtavioBonassi » Sex Jan 07, 2011 15:52
- 11 Respostas
- 8679 Exibições
- Última mensagem por OtavioBonassi

Dom Jan 09, 2011 22:47
Cálculo: Limites, Derivadas e Integrais
-
- Conceito Formal de Limites
por mindy » Qua Abr 06, 2011 14:50
- 2 Respostas
- 3636 Exibições
- Última mensagem por mindy

Sex Abr 08, 2011 14:15
Cálculo: Limites, Derivadas e Integrais
-
- [Conceito correto de 3ª proporcional]
por Jhenrique » Qua Jul 25, 2012 02:51
- 1 Respostas
- 1200 Exibições
- Última mensagem por DanielFerreira

Dom Ago 05, 2012 16:20
Geometria Plana
-
- [Limite] Conceito de Existência
por eli83 » Qua Out 10, 2012 10:33
- 4 Respostas
- 2568 Exibições
- Última mensagem por young_jedi

Qui Out 11, 2012 17:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



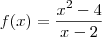 e
e  . Considere ainda que o domínio delas seja o mesmo:
. Considere ainda que o domínio delas seja o mesmo:  .
.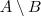 é o mesmo que
é o mesmo que  .
.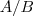 .
.
 e pede pra achar a derivada?? eu tentei jogar na formula
e pede pra achar a derivada?? eu tentei jogar na formula ![\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2} \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}](/latexrender/pictures/895a3c67e97b6b6a64a5af986d1ac5fd.png) e deu uns numeros muito extenso, é normal e eu tenho que simplificar depois, ou tem algo errado?
e deu uns numeros muito extenso, é normal e eu tenho que simplificar depois, ou tem algo errado?


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.