Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por Molina » Dom Jun 12, 2011 22:35
por Molina » Dom Jun 12, 2011 22:35
Preencha o diagrama colocando em cada círculo um dos algarismos de 0 a 9, sem repetição.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Qui Jul 14, 2011 20:07
por Molina » Qui Jul 14, 2011 20:07
Se alguém estiver tentando, manifeste-se!
Vou dar a dica de três algarismos:
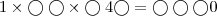

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Claudin » Sex Jul 15, 2011 14:31
por Claudin » Sex Jul 15, 2011 14:31
Molina,
Acho que encontrei um resultado plausível. Depois confere aqui.
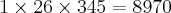
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Molina » Sex Jul 15, 2011 14:54
por Molina » Sex Jul 15, 2011 14:54
Claudin escreveu:Molina,
Acho que encontrei um resultado plausível. Depois confere aqui.
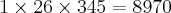
Abraço

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por FilipeCaceres » Sex Jul 15, 2011 19:55
por FilipeCaceres » Sex Jul 15, 2011 19:55
Olá Claudin,
Poste a sua solução também para que possamos usufruir da mesma.
Grande abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Sáb Jul 16, 2011 00:33
por Claudin » Sáb Jul 16, 2011 00:33
Analisei primeiramente, que a multiplicação entre os números, resultaria em um número no qual desse 0.
Como por exemplo 8x5; 6x5; 2x5.
E no entanto testei com valores menores possíveis, ou seja, colocando algarismos de menores valores para assumir o local da centena ou dezena do numeral, e assim foi umas 3 tentativas e encontrei a resposta.
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Sáb Jul 16, 2011 00:45
por FilipeCaceres » Sáb Jul 16, 2011 00:45
Olá Claudin,
Se você poder poste toda a sua solução.
Grande abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Sáb Jul 16, 2011 01:06
por Claudin » Sáb Jul 16, 2011 01:06
Foi o que eu disse Filipe
Fiz por tentativa, mas levando em consideração os algarismos finais para que a multiplicação tenha como resultado um numeral com algarismo das unidades igual a zero. E também levando em consideração, utilização de algarismos que possuem menor valor para a casa das centenas e dezenas. E utilizando esse método tentei 2 vezes e errei, e na terceira já encontrei uma resposta aceitável, e acabou sendo confirmada pelo Colaborador Molina.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por tenebroso » Qua Dez 18, 2013 23:18
por tenebroso » Qua Dez 18, 2013 23:18
faça uma caridade,um milagre lá em minha página...
-
tenebroso
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Dez 18, 2013 16:00
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: estudante
- Andamento: cursando
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Algarismos
por Valmel » Ter Out 23, 2012 18:23
- 1 Respostas
- 1684 Exibições
- Última mensagem por young_jedi

Ter Out 23, 2012 19:56
Aritmética
-
- algarismos!!!
por alissonade » Sex Abr 26, 2013 23:38
- 5 Respostas
- 3826 Exibições
- Última mensagem por alissonade

Dom Abr 28, 2013 19:10
Aritmética
-
- Soma dos algarismos
por thadeu » Qua Nov 18, 2009 16:19
- 4 Respostas
- 2537 Exibições
- Última mensagem por thadeu

Qua Nov 18, 2009 20:01
Álgebra Elementar
-
- Quantidade de Algarismos
por gustavowelp » Seg Jul 18, 2011 00:20
- 6 Respostas
- 3980 Exibições
- Última mensagem por Molina

Seg Jul 18, 2011 11:42
Estatística
-
- soma dos algarismos
por gokeafro » Sex Out 14, 2011 18:22
- 0 Respostas
- 1442 Exibições
- Última mensagem por gokeafro

Sex Out 14, 2011 18:22
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





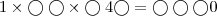


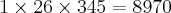









 .
.



