Isabela Sa escreveu:Nao consigo intender algumas coisas sobre limite
baseando nessa aula
http://www.youtube.com/watch?v=KSZNRo_o ... ideo_title
n consigo encontra resposta como o dono da aula encontro. algm ajuda com a resposta? tenho essa duvida e n consigo responder tem uns 3 dias.
Você está se referindo a
vídeo-aula "22. Cálculo I - Construção de Gráficos".
Em verdade, nessa vídeo-aula há o cálculo dos limites laterais:
(a)
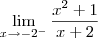
(b)
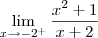
Para entender como calcular esses limites, é importante que você já tenha assistido a vídeo-aula "05. Cálculo I - Limites Infinitos".
Isabela Sa escreveu: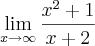
pela direita nem pela esquerda eu encontro os msm resultados
n consigo intender oq e feito na aula
Primeiro, esse limite não foi calculado "pela direita" e nem "pela esquerda".
Nessa vídeo-aula foram calculados os limites:
(c)

(d)
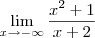
Atenção: não confunda "tender a mais infinito" com "tender pela direita", e nem "tender a menos infinito" com "tender pela esquerda".
Novamente, para entender o cálculo desses limites é importante que você já tenha assistido a vídeo-aula "06. Cálculo I - Limites no Infinito".
Uma maneira de resolvê-los, além das que já foram mencionadas aqui, é utilizar o que foi dito na própria vídeo-aula 22, que é através da divisão entre os polinômios x² + 1 e x + 2. Através dessa divisão, sabemos que:
x² + 1 = (x - 2)(x + 2) + 5
Desse modo, para o limite (c), temos que:


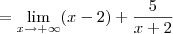
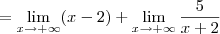
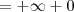

Utilizando uma ideia análoga, você obterá que o limite (d) é tal que:
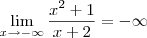
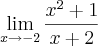
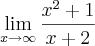


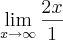





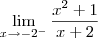
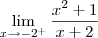

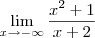


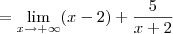
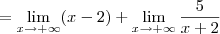
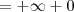

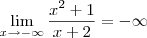
 .
.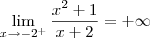 .
.