 por Andreyan » Ter Jul 12, 2011 17:55
por Andreyan » Ter Jul 12, 2011 17:55
Ola, estou com um exercício onde não consigo derivá-lo pela definição de limite.
![1/\sqrt[]{x} 1/\sqrt[]{x}](/latexrender/pictures/c12ce711d8629f1be83ca6188cdf64be.png)
?
Atravez da regra do quociente chego facilmente na resposta
![1/2x\sqrt[]{x} 1/2x\sqrt[]{x}](/latexrender/pictures/19712c4620b3d9365521fc797e706a25.png)
, porém talvez nao esteja manuseando corretamente pela definição de limite que é esta:

Tive essa questão na minha ultima prova e até agora não consegui resolvê-la. obrigado desde já.
-
Andreyan
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Jul 12, 2011 17:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em processos de produção
- Andamento: cursando
 por Andreyan » Ter Jul 12, 2011 17:59
por Andreyan » Ter Jul 12, 2011 17:59
![(1/\sqrt[]{x + h} - 1/\sqrt[]{x})1/h = 1/h\sqrt[]{x + h} - 1/h\sqrt[]{x} (1/\sqrt[]{x + h} - 1/\sqrt[]{x})1/h = 1/h\sqrt[]{x + h} - 1/h\sqrt[]{x}](/latexrender/pictures/388fa9365f9b7dae2ff8dc01eee2fceb.png)
Eu não passo dessa etapa.
-
Andreyan
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Jul 12, 2011 17:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em processos de produção
- Andamento: cursando
 por LuizAquino » Ter Jul 12, 2011 18:45
por LuizAquino » Ter Jul 12, 2011 18:45
Seja a função

.
Pela definição de derivada, temos que:

Efetuando-se a subtração entre as frações, obtemos:
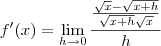
Mas, isso é o mesmo que:
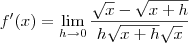
Para terminar de resolver esse limite, multiplique tanto o numerador quanto o denominador por
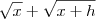
.
Vale lembrar que a resposta final será:
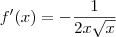
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Andreyan » Qua Jul 13, 2011 13:05
por Andreyan » Qua Jul 13, 2011 13:05
-
Andreyan
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Jul 12, 2011 17:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em processos de produção
- Andamento: cursando
 por LuizAquino » Qua Jul 13, 2011 15:27
por LuizAquino » Qua Jul 13, 2011 15:27
Você errou o sinal.
![\frac{\sqrt{x} - \sqrt{x + h}}{h\sqrt{x + h}\sqrt{x}} \cdot \frac{\sqrt{x} + \sqrt{x + h}}{\sqrt{x} + \sqrt{x + h}} = \frac{x - (x + h)}{hx\sqrt{x + h} + h(x + h)\sqrt{x}} = \frac{-h}{h[x\sqrt{x + h} + (x + h)\sqrt{x}]} \frac{\sqrt{x} - \sqrt{x + h}}{h\sqrt{x + h}\sqrt{x}} \cdot \frac{\sqrt{x} + \sqrt{x + h}}{\sqrt{x} + \sqrt{x + h}} = \frac{x - (x + h)}{hx\sqrt{x + h} + h(x + h)\sqrt{x}} = \frac{-h}{h[x\sqrt{x + h} + (x + h)\sqrt{x}]}](/latexrender/pictures/9c777a4296984421cf5464de9e6fa003.png)
Andreyan escreveu:sinto muita dificuldade no momento que vc disse de multiplicar o numerador e o denominador, pela mesma expressão. Não por multiplicar, mas sim "pelo que multiplicar", vários limites me atrapalham por causa disso, principalmente com radicais, alguma dica?
Dica: revisar os conteúdos do ensino fundamental e médio. Um bom lugar para começar é o canal do Nerckie no YouTube:
http://www.youtube.com/nerckieAndreyan escreveu:eu nem sei qual o nome desta operação..rs.
No caso desse exercício, procure por "racionalização de denominadores".
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada pela definição de limite
por SheylaTamarossi » Dom Jun 12, 2011 11:27
- 6 Respostas
- 8329 Exibições
- Última mensagem por Fabio Cabral

Seg Jun 13, 2011 12:07
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela Definiçao
por PeIdInHu » Sáb Mai 22, 2010 17:24
- 1 Respostas
- 2199 Exibições
- Última mensagem por admin

Sáb Mai 22, 2010 18:24
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definiçao
por tumiattibrz » Sex Mai 27, 2011 17:17
- 3 Respostas
- 2513 Exibições
- Última mensagem por LuizAquino

Sáb Mai 28, 2011 12:28
Cálculo: Limites, Derivadas e Integrais
-
- derivada pela definiçao
por paula luna » Sex Jun 10, 2011 04:41
- 2 Respostas
- 2279 Exibições
- Última mensagem por Fabio Cabral

Sex Jun 10, 2011 11:23
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definição
por core » Qua Out 16, 2013 02:15
- 1 Respostas
- 1752 Exibições
- Última mensagem por Taka

Sáb Nov 02, 2013 21:26
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![1/\sqrt[]{x} 1/\sqrt[]{x}](/latexrender/pictures/c12ce711d8629f1be83ca6188cdf64be.png) ?
?![1/2x\sqrt[]{x} 1/2x\sqrt[]{x}](/latexrender/pictures/19712c4620b3d9365521fc797e706a25.png) , porém talvez nao esteja manuseando corretamente pela definição de limite que é esta:
, porém talvez nao esteja manuseando corretamente pela definição de limite que é esta: 

![1/\sqrt[]{x} 1/\sqrt[]{x}](/latexrender/pictures/c12ce711d8629f1be83ca6188cdf64be.png) ?
?![1/2x\sqrt[]{x} 1/2x\sqrt[]{x}](/latexrender/pictures/19712c4620b3d9365521fc797e706a25.png) , porém talvez nao esteja manuseando corretamente pela definição de limite que é esta:
, porém talvez nao esteja manuseando corretamente pela definição de limite que é esta: 

![(1/\sqrt[]{x + h} - 1/\sqrt[]{x})1/h = 1/h\sqrt[]{x + h} - 1/h\sqrt[]{x} (1/\sqrt[]{x + h} - 1/\sqrt[]{x})1/h = 1/h\sqrt[]{x + h} - 1/h\sqrt[]{x}](/latexrender/pictures/388fa9365f9b7dae2ff8dc01eee2fceb.png)

 .
.
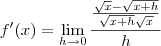
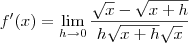
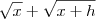 .
.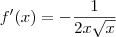

![\frac{\sqrt[]{x} - \sqrt[]{x + h}}{h\sqrt[]{x + h}\sqrt[]{x}} .
\frac{\sqrt[]{x} + \sqrt[]{x + h}}{\sqrt[]{x} + \sqrt[]{x + h}} \frac{\sqrt[]{x} - \sqrt[]{x + h}}{h\sqrt[]{x + h}\sqrt[]{x}} .
\frac{\sqrt[]{x} + \sqrt[]{x + h}}{\sqrt[]{x} + \sqrt[]{x + h}}](/latexrender/pictures/ec05508f00fe270d7773c00a41a470b0.png)
![\frac{x - x + h}{hx\sqrt[]{x + h} + h(x + h)\sqrt[]{x}} \frac{x - x + h}{hx\sqrt[]{x + h} + h(x + h)\sqrt[]{x}}](/latexrender/pictures/e6e8a087c5c2e2b27604efbc678affeb.png)
![\frac{h}{h (x.\sqrt[]{x + h} + (x + h).\sqrt[]{x}} \frac{h}{h (x.\sqrt[]{x + h} + (x + h).\sqrt[]{x}}](/latexrender/pictures/88e8bf8dfae8208c4f348485337521a7.png)
![\frac{1}{x.\sqrt[]{x + h} + (x + h).\sqrt[]{x}} \frac{1}{x.\sqrt[]{x + h} + (x + h).\sqrt[]{x}}](/latexrender/pictures/6eb9aca798cf913eb7f7eda3960b9e3d.png)
![\frac{1}{x.\sqrt[]{x} + x.\sqrt[]{x}} \frac{1}{x.\sqrt[]{x} + x.\sqrt[]{x}}](/latexrender/pictures/ca01dcc2217235dd00f30cca55307cc4.png)
![\frac{1}{2x . \sqrt[]{x}} \frac{1}{2x . \sqrt[]{x}}](/latexrender/pictures/a318488b88e055f6b57ca803a10516ca.png)

![\frac{\sqrt{x} - \sqrt{x + h}}{h\sqrt{x + h}\sqrt{x}} \cdot \frac{\sqrt{x} + \sqrt{x + h}}{\sqrt{x} + \sqrt{x + h}} = \frac{x - (x + h)}{hx\sqrt{x + h} + h(x + h)\sqrt{x}} = \frac{-h}{h[x\sqrt{x + h} + (x + h)\sqrt{x}]} \frac{\sqrt{x} - \sqrt{x + h}}{h\sqrt{x + h}\sqrt{x}} \cdot \frac{\sqrt{x} + \sqrt{x + h}}{\sqrt{x} + \sqrt{x + h}} = \frac{x - (x + h)}{hx\sqrt{x + h} + h(x + h)\sqrt{x}} = \frac{-h}{h[x\sqrt{x + h} + (x + h)\sqrt{x}]}](/latexrender/pictures/9c777a4296984421cf5464de9e6fa003.png)

