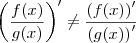por Isabela Sa » Ter Jul 12, 2011 11:46
por Isabela Sa » Ter Jul 12, 2011 11:46
Sendo:

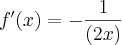

tenho duvida se esta certo ou n?
pq eu vi o video de um professor do forum
q tava com valor diferente ai n intendi
http://www.youtube.com/watch?v=KL08c3ao ... ure=relmfuobrigada
-
Isabela Sa
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jun 23, 2011 12:24
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por LuizAquino » Ter Jul 12, 2011 14:55
por LuizAquino » Ter Jul 12, 2011 14:55
O que você fez está errado.
Para derivar a função

é necessário usar a
regra do quociente. Sendo assim, temos que:
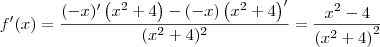
Se você quiser calcular a segunda derivada, então terá que aplicar a
regra do quociente novamente. Ou seja, temos que:
![f^{\prime\prime}(x) = \frac{\left(x^2 - 4\right)^\prime \left(x^2 + 4\right)^2 - \left(x^2 - 4\right)\left[\left(x^2 + 4\right)^2\right]^\prime}{\left[\left(x^2 + 4\right)^2\right]^2} = \frac{-2x^3+24x}{\left(x^2 + 4\right)^3} f^{\prime\prime}(x) = \frac{\left(x^2 - 4\right)^\prime \left(x^2 + 4\right)^2 - \left(x^2 - 4\right)\left[\left(x^2 + 4\right)^2\right]^\prime}{\left[\left(x^2 + 4\right)^2\right]^2} = \frac{-2x^3+24x}{\left(x^2 + 4\right)^3}](/latexrender/pictures/c7876d5870608339becbe6294b1758d4.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Isabela Sa » Qua Jul 13, 2011 00:35
por Isabela Sa » Qua Jul 13, 2011 00:35
n intendi o pq de usar essa regra do quociente
derivando normalmente n da certo n?
thanks
-
Isabela Sa
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jun 23, 2011 12:24
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por Paulo4114 » Qua Jul 13, 2011 02:33
por Paulo4114 » Qua Jul 13, 2011 02:33
Olá!
Você pode resolver este exercicio de 2 formas. A primeira e mais simples é utilizando a própria regra do quociente ou derivada do quociente.
Mas se você não percebeu o porquê de usa-la, então, terá de adquirir mais conceitos.
Não posto aqui porque tornar-se-ia muito extenso, por isso:
Visite: aprendermmatematica.blogspot.com/
ou envie email para:
isistelv@gmail.compara que possamos saber que está a procura de compreender a resolução deste(s) exercicios.
Obrigado e bom estudo
-
Paulo4114
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 13, 2011 02:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eletronica
- Andamento: formado
 por Molina » Qua Jul 13, 2011 08:16
por Molina » Qua Jul 13, 2011 08:16
Bom dia, Isabela.
Isabela Sa escreveu:n intendi o pq de usar essa regra do quociente
derivando normalmente n da certo n?
thanks
Você está se confundindo. A derivada do quociente não é o quociente da derivada:
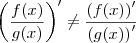
Procure no seu livro (ou até mesmo na internet) sobre a
Regra do Produto.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizAquino » Qua Jul 13, 2011 10:07
por LuizAquino » Qua Jul 13, 2011 10:07
Na
vídeo-aula "12. Cálculo I - Regras Operatórias das Derivadas" é explicado essa regra.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Dúvida ao calcular uma derivada...
por dileivas » Ter Mai 01, 2012 09:54
- 2 Respostas
- 2257 Exibições
- Última mensagem por dileivas

Ter Mai 01, 2012 17:18
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] Duvida em derivada da definição.
por paulohenrique_ » Dom Dez 09, 2012 16:05
- 1 Respostas
- 1930 Exibições
- Última mensagem por young_jedi

Dom Dez 09, 2012 18:12
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em derivada
por luiz3107 » Seg Ago 23, 2010 02:50
- 2 Respostas
- 1913 Exibições
- Última mensagem por luiz3107

Seg Ago 23, 2010 15:15
Cálculo: Limites, Derivadas e Integrais
-
- Duvida Derivada.
por Bio10ct » Qua Abr 18, 2012 09:17
- 1 Respostas
- 1050 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 11:58
Cálculo: Limites, Derivadas e Integrais
-
- Derivada {dúvida}
por Danilo » Ter Abr 23, 2013 11:51
- 1 Respostas
- 1023 Exibições
- Última mensagem por young_jedi

Ter Abr 23, 2013 12:04
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

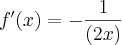



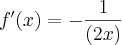


 é necessário usar a regra do quociente. Sendo assim, temos que:
é necessário usar a regra do quociente. Sendo assim, temos que: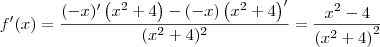
![f^{\prime\prime}(x) = \frac{\left(x^2 - 4\right)^\prime \left(x^2 + 4\right)^2 - \left(x^2 - 4\right)\left[\left(x^2 + 4\right)^2\right]^\prime}{\left[\left(x^2 + 4\right)^2\right]^2} = \frac{-2x^3+24x}{\left(x^2 + 4\right)^3} f^{\prime\prime}(x) = \frac{\left(x^2 - 4\right)^\prime \left(x^2 + 4\right)^2 - \left(x^2 - 4\right)\left[\left(x^2 + 4\right)^2\right]^\prime}{\left[\left(x^2 + 4\right)^2\right]^2} = \frac{-2x^3+24x}{\left(x^2 + 4\right)^3}](/latexrender/pictures/c7876d5870608339becbe6294b1758d4.png)