 por Cleyson007 » Seg Jul 11, 2011 22:02
por Cleyson007 » Seg Jul 11, 2011 22:02
Utilizando o
Teorema do Confronto prove que:
Sejam
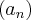
,

e
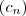
sequências tais que
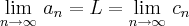
. Se existe
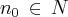
tal que
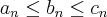
para todo

, então
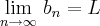
.
Agradeço quem puder me ajudar.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Ter Jul 12, 2011 00:26
por MarceloFantini » Ter Jul 12, 2011 00:26
Mas isso é o próprio teorema do confronto. Você está estudando Análise Matemática, Cleyson?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Ter Jul 12, 2011 08:58
por Cleyson007 » Ter Jul 12, 2011 08:58
Bom dia Fantini!
Estou estudando Análise Real e tenho muita dificuldade nesses tipos de exercícios que pedem para provar, mostrar..
Fantini, você possui algum material que explique detalhadamente os estudo das sequências (se são convergentes ou divergentes)?
Enfim, o que você puder me ajudar ficarei muito agradecido.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Ter Jul 12, 2011 09:05
por MarceloFantini » Ter Jul 12, 2011 09:05
Existem livros bons de Análise que você pode consultar, em português o clássico é o "Um Curso de Análise", volume 1 já é o suficiente. O bom é que é barato, apenas 25 reais na livraria da SBM (Sociedade Brasileira de Matemática). Lá deve ter a demonstração deste teorema e as respostas para suas outras perguntas. Existem livros em inglês também, como Principles of Mathematical Analysis do Rudin, Analysis do Serge Lang pela editora Springer, e muitos outros.
É bom que adquira prática nestes exercícios de demonstrar ou provar pois eles estão no coração da matemática, e um verdadeiro matemático tem que ser bem treinado nisto. Talvez no comece isso pareça assustador, mas é uma questão de prática, assim como a maioria dos assuntos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema do Confronto
por Claudin » Qua Mai 25, 2011 19:51
- 3 Respostas
- 3437 Exibições
- Última mensagem por LuizAquino

Qua Mai 25, 2011 21:12
Cálculo: Limites, Derivadas e Integrais
-
- Teorema do confronto
por jemourafer » Dom Abr 01, 2012 20:23
- 1 Respostas
- 1674 Exibições
- Última mensagem por NMiguel

Dom Abr 01, 2012 21:00
Cálculo: Limites, Derivadas e Integrais
-
- [limite]teorema do confronto
por gabriel feron » Dom Mai 06, 2012 20:25
- 1 Respostas
- 1820 Exibições
- Última mensagem por MarceloFantini

Dom Mai 06, 2012 22:53
Cálculo: Limites, Derivadas e Integrais
-
- LIMITES - Teorema do confronto
por paola-carneiro » Dom Jun 03, 2012 20:53
- 1 Respostas
- 1905 Exibições
- Última mensagem por Fabio Wanderley

Seg Jun 04, 2012 02:45
Cálculo: Limites, Derivadas e Integrais
-
- [Resolução de limite] Teorema do Confronto
por nievag » Ter Mai 13, 2014 00:58
- 1 Respostas
- 2132 Exibições
- Última mensagem por e8group

Ter Mai 13, 2014 10:50
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
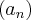 ,
,  e
e 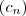 sequências tais que
sequências tais que 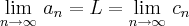 . Se existe
. Se existe 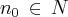 tal que
tal que 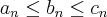 para todo
para todo  , então
, então 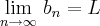 .
.
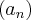 ,
,  e
e 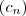 sequências tais que
sequências tais que 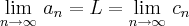 . Se existe
. Se existe 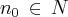 tal que
tal que 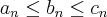 para todo
para todo  , então
, então 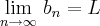 .
.




