Dado: x=Dx/D
Tipo I: dois sabonetes, uma escova de dente e dois cremes dentais. (=8,70)
Tipo II: Tres sabonetes, uma escova de dente e um creme dental (=8,20)
Tipo III: dois sabonetes, duas escovas de dente e dois cremes dentais. (=10,40)
____
O que eu resolvi:
2s+e+2c=8,70
3s+e+2c=8,20
2s+2e+2c=10,40
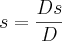


Encontrei o valor de D, que pelos meus calculos é 4.
E para encontrar o valor de De, Dc,Ds. Como prossigo?
Desdejá obrigado!!


 ,
,  e
e  são os determinantes dos coeficientes com a coluna da variável substituida por uma coluna que tem os valores do lado direito. Exemplo:
são os determinantes dos coeficientes com a coluna da variável substituida por uma coluna que tem os valores do lado direito. Exemplo: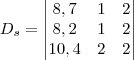




 .
.
 :
: