![\lim_{x \to \ 3} \frac {\sqrt[3]{x} - \sqrt[3]{3}}{x - 3} \lim_{x \to \ 3} \frac {\sqrt[3]{x} - \sqrt[3]{3}}{x - 3}](/latexrender/pictures/a66a48264a940e9634e60ab7da0a14d2.png)
![\lim_{x \to \ 2} \frac {\sqrt[4]{x} - \sqrt[4]{2}}{x - 2} \lim_{x \to \ 2} \frac {\sqrt[4]{x} - \sqrt[4]{2}}{x - 2}](/latexrender/pictures/527d8ac629ce0c254907486d3200bdc6.png)
Segundo o Guidorrizi vol.1 (Um curso de Calculo), o resultado do primeiro limite é
![\frac {1}{3 \sqrt[3]{9}} \frac {1}{3 \sqrt[3]{9}}](/latexrender/pictures/3d29fabe9ecadee65aa4de36a307d1f4.png) e o segundo é
e o segundo é ![\frac {1}{4 \sqrt[4]{8}} \frac {1}{4 \sqrt[4]{8}}](/latexrender/pictures/062624c0fe5f402c96d2fcac8207f50b.png) mas não sei como faço para alcançar esses resultados.
mas não sei como faço para alcançar esses resultados.
![\lim_{x \to \ 3} \frac {\sqrt[3]{x} - \sqrt[3]{3}}{x - 3} \lim_{x \to \ 3} \frac {\sqrt[3]{x} - \sqrt[3]{3}}{x - 3}](/latexrender/pictures/a66a48264a940e9634e60ab7da0a14d2.png)
![\lim_{x \to \ 2} \frac {\sqrt[4]{x} - \sqrt[4]{2}}{x - 2} \lim_{x \to \ 2} \frac {\sqrt[4]{x} - \sqrt[4]{2}}{x - 2}](/latexrender/pictures/527d8ac629ce0c254907486d3200bdc6.png)
![\frac {1}{3 \sqrt[3]{9}} \frac {1}{3 \sqrt[3]{9}}](/latexrender/pictures/3d29fabe9ecadee65aa4de36a307d1f4.png) e o segundo é
e o segundo é ![\frac {1}{4 \sqrt[4]{8}} \frac {1}{4 \sqrt[4]{8}}](/latexrender/pictures/062624c0fe5f402c96d2fcac8207f50b.png) mas não sei como faço para alcançar esses resultados.
mas não sei como faço para alcançar esses resultados.


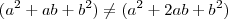
 , como explicado acima.
, como explicado acima.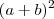 , como você mesmo afirmou:
, como você mesmo afirmou: gabrielspadon escreveu:(a²+2ab+b²) = (a+b)²
gabrielspadon escreveu:Por que (a²+ab+b²) e não (a²+2ab+b²) = (a+b)²?
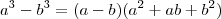



 ?
? ao invés de
ao invés de 


![\lim_{x \to \ p} \frac {\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \frac {1}{n \sqrt[n]{p^{n-1}}} \lim_{x \to \ p} \frac {\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \frac {1}{n \sqrt[n]{p^{n-1}}}](/latexrender/pictures/6fc60b8d7b944766d12e09704fed7727.png)
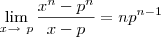
![\lim_{x \to \ p} \frac {\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to \ p} \frac {1}{\sqrt[n]{x^{n-1}} - \sqrt[n]{p^{n-1}}} \lim_{x \to \ p} \frac {\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to \ p} \frac {1}{\sqrt[n]{x^{n-1}} - \sqrt[n]{p^{n-1}}}](/latexrender/pictures/c007c7fcdbdc25fae60db78572571946.png)

![\sqrt[n]{x} \sqrt[n]{x}](/latexrender/pictures/13fcbed8bcac58d95c0cb989f3aca2de.png) .
.
Renato_RJ escreveu:Em resumo, você acabou de determinar a derivada da função no ponto P...




gabrielspadon escreveu:Obrigado, consegui calcular e entender o primeiro limite, mas ainda não consegui enxergar qual produto notável se encaixa no segundo limite...
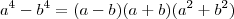

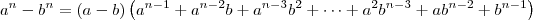 , com n natural e n > 1.
, com n natural e n > 1.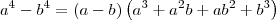


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)