 por jamiel » Sáb Jul 02, 2011 17:47
por jamiel » Sáb Jul 02, 2011 17:47
Determine m para que exista o arco x, satisfazendo as igualdades:
d)

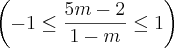
Resolução:

Mas no gabarito consta
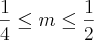
Na minha resolução, ficaria
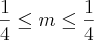
Fiquei sem entender essa. Alguém para dar uma dica?
Editado pela última vez por
jamiel em Sáb Jul 02, 2011 18:58, em um total de 1 vez.
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Sáb Jul 02, 2011 18:59
por jamiel » Sáb Jul 02, 2011 18:59
Se vc se referiu a desigualdade total, tá lá na parte de cima, consertei!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Sáb Jul 02, 2011 19:06
por jamiel » Sáb Jul 02, 2011 19:06
A outra parte " m?1/2", eu fiz da mesma forma
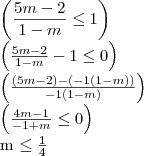
Essa seria a outra parte da desigualdade!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Sáb Jul 02, 2011 19:14
por MarceloFantini » Sáb Jul 02, 2011 19:14
Você está errando em algumas contas, veja:
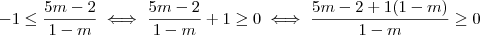
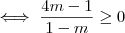
Assim,

. Para o outro lado:


Logo,
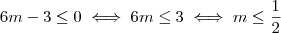
Note que

sempre, mas como não está no intervalo, não há problema.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Sáb Jul 02, 2011 19:27
por jamiel » Sáb Jul 02, 2011 19:27
Mas, vc não multiplicou o "-1" na segunda desigualdade. Continuo sem entender!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Sáb Jul 02, 2011 19:42
por jamiel » Sáb Jul 02, 2011 19:42
Putz! Percebi. É q não estava lembrado das inequações. Multiplica apenas o denominador posto na parte de cima da divisão. Eu pensava q multiplicava o denominador também!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida na Resolução de uma Função
 por brunnomaia » Dom Mar 06, 2011 11:07
por brunnomaia » Dom Mar 06, 2011 11:07
- 2 Respostas
- 1808 Exibições
- Última mensagem por brunnomaia

Dom Mar 06, 2011 11:53
Funções
-
- Dúvida - resolução função !
 por jamiel » Qui Mai 26, 2011 18:07
por jamiel » Qui Mai 26, 2011 18:07
- 11 Respostas
- 5914 Exibições
- Última mensagem por jamiel

Qui Mai 26, 2011 22:31
Funções
-
- Função Exponencial - Dúvida na resolução!
por jamiel » Dom Mai 15, 2011 14:09
- 1 Respostas
- 4770 Exibições
- Última mensagem por Claudin

Dom Mai 15, 2011 14:21
Funções
-
- Retângulo - função(resolução-dúvida)
por jamiel » Seg Mai 23, 2011 14:44
- 2 Respostas
- 4026 Exibições
- Última mensagem por jamiel

Seg Mai 23, 2011 21:39
Funções
-
- Dúvida - resolução(função inversa)
por jamiel » Ter Jun 14, 2011 18:49
- 1 Respostas
- 1465 Exibições
- Última mensagem por DanielFerreira

Qui Jun 16, 2011 16:00
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

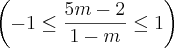

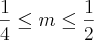
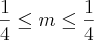


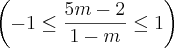

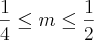
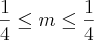



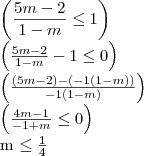

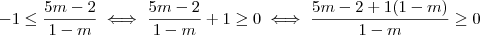
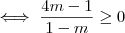
 . Para o outro lado:
. Para o outro lado:

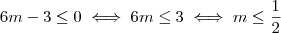
 sempre, mas como não está no intervalo, não há problema.
sempre, mas como não está no intervalo, não há problema.



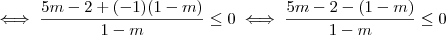





![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)