 por Raphael Feitas10 » Sex Jul 01, 2011 23:54
por Raphael Feitas10 » Sex Jul 01, 2011 23:54
O produto de dois numeros é 250 e o seu mdc é 5.Calcule esses numeros.R: 10 e 25
Brother fiz assim mas ñ obtive êxito me ajuda aew parceiro desde ja agradecido.
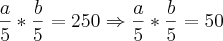
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Molina » Sáb Jul 02, 2011 17:37
por Molina » Sáb Jul 02, 2011 17:37
Boa tarde, Raphael.
Sejam
a e
b esses números. Pelo enunciado temos que:
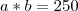
e
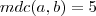
Como o mdc desses dois números é 5 podemos escrever
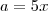
e
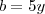
, com
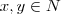
. Assim:
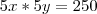
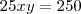

Como x e y são naturais isso nos diz que eles serão 1 e 10 ou 2 e 5. Testando-os, chegamos a conclusão que

e

.
Mas,
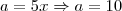
e
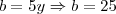

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
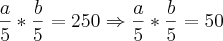

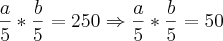

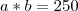
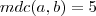
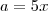 e
e 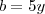 , com
, com 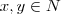 . Assim:
. Assim: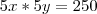
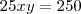

 e
e  .
.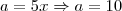 e
e 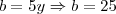



 .
.



