 por luiz syncode » Sex Jul 01, 2011 12:07
por luiz syncode » Sex Jul 01, 2011 12:07
Peço ajuda aos amigos daqui do forum para me ajudar com isto:
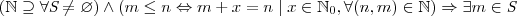
Escrevi corretamente? O que vcs entendem por isso?
Posso utilizar o "e" lógico (

) desta forma?
O que vcs sugerem para que eu possa definir que para todo conjunto não vazio pertencente ao conjunto dos numeros naturais existe um elemento minimo?
-
luiz syncode
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Jul 01, 2011 12:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica, Fisica, Computação, Lógica
- Andamento: cursando
 por LuizAquino » Sáb Jul 02, 2011 13:08
por LuizAquino » Sáb Jul 02, 2011 13:08
luiz syncode escreveu:Peço ajuda aos amigos daqui do forum para me ajudar com isto:
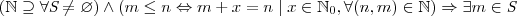
Escrevi corretamente?
Não escreveu.
luiz syncode escreveu:O que vcs entendem por isso?
Literalmente, está escrito algo como:
"Se

contém ou é igual para todo S não vazio e

se, e somente se, m + x = n, com x pertencente a
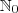
, para todo (n, m) pertencentes a

, então existe m pertencente a S".
Perceba como esse texto está sem sentido!
luiz syncode escreveu:Posso utilizar o "e" lógico (

) desta forma?
Nesse caso, como você viu acima, ficou ruim.
luiz syncode escreveu:O que vcs sugerem para que eu possa definir que para todo conjunto não vazio pertencente ao conjunto dos numeros naturais existe um elemento minimo?
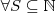
, com
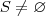
,

tal que

,
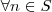
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sáb Jul 02, 2011 18:45
por MarceloFantini » Sáb Jul 02, 2011 18:45
Luiz, aqui vai um comentário pessoal: existem certas expressões que são muito complicadas de serem escritas simbolicamente, portanto em vez de ajudar a compreensão elas dificultam, o que é considerado ruim em muitos casos. Nós procuramos sempre deixar um texto da maneira mais objetiva e clara, e um texto quase que puramente simbólico vai contra essa idéia.
Apenas relembrando, um comentário pessoal. Não pretendo ser ofensivo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por luiz syncode » Sáb Jul 02, 2011 22:14
por luiz syncode » Sáb Jul 02, 2011 22:14
Muitíssimo obrigado aos senhores LuizAquino e MarceloFantini pelas respostas.
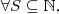
com
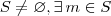
tal que
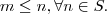
Isto realmente está bem melhor.
Mas e se eu quiser mostrar que para

ser verdadeiro, devemos ter que
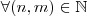
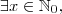
tal que

Como eu poderia mostrar isso, também, mas de forma correta?
Eu também acho muito complicado escrever simbolicamente e também acho que todos os textos que encontro sobre matemática poderiam ter expressões simbólicas, desde que ninguem se esquecesse de "traduzi-las" para o portugues. Mas como isso não acontece, sou obrigado a aprender muito bem a simbologia matemática para entender os textos com os quais tenho me deparado.
Estou me obrigando, apartir de hoje, entender bem a simbologia porque eu adoro matemática. Assim como eu aprendi um pouco de ingles vivenciando ele num país extrangeiro, eu só poderei aprender a simbologia matemática aqui, com vocês, vivenciando e sendo corrigido. Muito obrigado novamente a vcs.
-
luiz syncode
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Jul 01, 2011 12:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica, Fisica, Computação, Lógica
- Andamento: cursando
 por LuizAquino » Ter Jul 05, 2011 23:04
por LuizAquino » Ter Jul 05, 2011 23:04
luiz syncode escreveu:Eu também acho muito complicado escrever simbolicamente e também acho que todos os textos que encontro sobre matemática poderiam ter expressões simbólicas, desde que ninguem se esquecesse de "traduzi-las" para o portugues. Mas como isso não acontece, sou obrigado a aprender muito bem a simbologia matemática para entender os textos com os quais tenho me deparado.
Em qualquer área do conhecimento humano, é necessário que os estudantes e profissionais dessa área conheçam os termos técnicos e simbologias utilizadas. Com a Matemática isso não é diferente. É obrigação do leitor fazer a tradução do que está escrito simbolicamente para a sua língua materna.
Aliás, a Matemática é talvez a única área em que a maior parte de seus textos podem ser lidos por nativos de qualquer língua. Não importa em que língua você é nativo, se você estuda (ou trabalha com Matemática) saberá o que significa o texto abaixo:
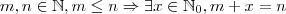
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Linguagem Matemática
 por Claudin » Qua Set 07, 2011 21:47
por Claudin » Qua Set 07, 2011 21:47
- 6 Respostas
- 2747 Exibições
- Última mensagem por Claudin

Qui Set 08, 2011 02:13
Inequações
-
- Linguagem algébrica
por Renatinha » Seg Nov 01, 2010 01:22
- 7 Respostas
- 5347 Exibições
- Última mensagem por girl

Ter Nov 02, 2010 14:06
Álgebra Elementar
-
- Linguagem algébrica
por Renatinha » Ter Nov 02, 2010 14:13
- 4 Respostas
- 4465 Exibições
- Última mensagem por Dinora

Dom Nov 07, 2010 23:24
Álgebra Elementar
-
- matemática- algebra
por zenildo » Sex Mai 31, 2013 16:08
- 0 Respostas
- 588 Exibições
- Última mensagem por zenildo

Sex Mai 31, 2013 16:08
Álgebra Elementar
-
- [Álgebra]Livro Problemas Selecionados de Matemática(Gandhi)
por PauloLima » Sáb Ago 24, 2013 17:50
- 0 Respostas
- 1876 Exibições
- Última mensagem por PauloLima

Sáb Ago 24, 2013 17:50
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
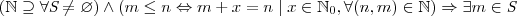
 ) desta forma?
) desta forma?
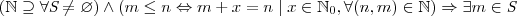
 ) desta forma?
) desta forma?
 contém ou é igual para todo S não vazio e
contém ou é igual para todo S não vazio e  se, e somente se, m + x = n, com x pertencente a
se, e somente se, m + x = n, com x pertencente a 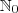 , para todo (n, m) pertencentes a
, para todo (n, m) pertencentes a  , então existe m pertencente a S".
, então existe m pertencente a S".) desta forma?
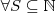 , com
, com 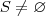 ,
,  tal que
tal que  ,
, 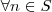 .
.


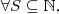 com
com 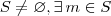 tal que
tal que 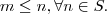
 ser verdadeiro, devemos ter que
ser verdadeiro, devemos ter que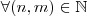
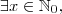 tal que
tal que 

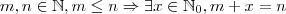 .
.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.