 por Claudin » Sex Jul 01, 2011 03:27
por Claudin » Sex Jul 01, 2011 03:27
Fazendo exercícios do livro de Guidorizzi
Deparei com tal dúvida:
![\lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3} \lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}](/latexrender/pictures/0ebbfecbd124cb8629e1df0405735d32.png)
Em que desenvolvendo obtive:
![\lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}. \frac{\sqrt[3]{x}+\sqrt[3]{3}}{\sqrt[3]{x}+\sqrt[3]{3}} \lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}. \frac{\sqrt[3]{x}+\sqrt[3]{3}}{\sqrt[3]{x}+\sqrt[3]{3}}](/latexrender/pictures/af3e6a2bfbecbeaf0c5512cda403cb59.png)
![\lim_{x\rightarrow3}\frac{(x-3)}{(x-3)(\sqrt[3]{x}+\sqrt[3]{3})} \lim_{x\rightarrow3}\frac{(x-3)}{(x-3)(\sqrt[3]{x}+\sqrt[3]{3})}](/latexrender/pictures/7ba967464107aaaca33295ba37e8de1d.png)
![\lim_{x\rightarrow3}\frac{1}{\sqrt[3]{x}+\sqrt[3]{3}}= \frac{1}{\sqrt[3]{3}+\sqrt[3]{3}} = \frac{1}{2\sqrt[3]{3}} \lim_{x\rightarrow3}\frac{1}{\sqrt[3]{x}+\sqrt[3]{3}}= \frac{1}{\sqrt[3]{3}+\sqrt[3]{3}} = \frac{1}{2\sqrt[3]{3}}](/latexrender/pictures/378e05cf52f461fab9b27a29857c9105.png)
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Sex Jul 01, 2011 03:29
por Claudin » Sex Jul 01, 2011 03:29
Porém a resposta correta seguindo o gabarito do livro seria
![\frac{1}{3\sqrt[3]{9}} \frac{1}{3\sqrt[3]{9}}](/latexrender/pictures/e8db584c1c98bc0938f8d512cad4e766.png)
Alguém poderia confirmar a resposta correta e se possível mostrar onde eu errei.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Fabio Cabral » Sex Jul 01, 2011 11:40
por Fabio Cabral » Sex Jul 01, 2011 11:40
Claudinho, não há necessidade de multiplicar pelo conjugado.
Apenas aplique o produto notável no denominador e aplique o limite.
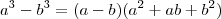
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Claudin » Qua Jul 20, 2011 16:18
por Claudin » Qua Jul 20, 2011 16:18
Correto Fábio Cabral.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Qua Jul 20, 2011 16:23
por Claudin » Qua Jul 20, 2011 16:23
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6642 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5117 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7257 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4434 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3} \lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}](/latexrender/pictures/0ebbfecbd124cb8629e1df0405735d32.png)
![\lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}. \frac{\sqrt[3]{x}+\sqrt[3]{3}}{\sqrt[3]{x}+\sqrt[3]{3}} \lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}. \frac{\sqrt[3]{x}+\sqrt[3]{3}}{\sqrt[3]{x}+\sqrt[3]{3}}](/latexrender/pictures/af3e6a2bfbecbeaf0c5512cda403cb59.png)
![\lim_{x\rightarrow3}\frac{(x-3)}{(x-3)(\sqrt[3]{x}+\sqrt[3]{3})} \lim_{x\rightarrow3}\frac{(x-3)}{(x-3)(\sqrt[3]{x}+\sqrt[3]{3})}](/latexrender/pictures/7ba967464107aaaca33295ba37e8de1d.png)
![\lim_{x\rightarrow3}\frac{1}{\sqrt[3]{x}+\sqrt[3]{3}}= \frac{1}{\sqrt[3]{3}+\sqrt[3]{3}} = \frac{1}{2\sqrt[3]{3}} \lim_{x\rightarrow3}\frac{1}{\sqrt[3]{x}+\sqrt[3]{3}}= \frac{1}{\sqrt[3]{3}+\sqrt[3]{3}} = \frac{1}{2\sqrt[3]{3}}](/latexrender/pictures/378e05cf52f461fab9b27a29857c9105.png)

![\lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3} \lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}](/latexrender/pictures/0ebbfecbd124cb8629e1df0405735d32.png)
![\lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}. \frac{\sqrt[3]{x}+\sqrt[3]{3}}{\sqrt[3]{x}+\sqrt[3]{3}} \lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}. \frac{\sqrt[3]{x}+\sqrt[3]{3}}{\sqrt[3]{x}+\sqrt[3]{3}}](/latexrender/pictures/af3e6a2bfbecbeaf0c5512cda403cb59.png)
![\lim_{x\rightarrow3}\frac{(x-3)}{(x-3)(\sqrt[3]{x}+\sqrt[3]{3})} \lim_{x\rightarrow3}\frac{(x-3)}{(x-3)(\sqrt[3]{x}+\sqrt[3]{3})}](/latexrender/pictures/7ba967464107aaaca33295ba37e8de1d.png)
![\lim_{x\rightarrow3}\frac{1}{\sqrt[3]{x}+\sqrt[3]{3}}= \frac{1}{\sqrt[3]{3}+\sqrt[3]{3}} = \frac{1}{2\sqrt[3]{3}} \lim_{x\rightarrow3}\frac{1}{\sqrt[3]{x}+\sqrt[3]{3}}= \frac{1}{\sqrt[3]{3}+\sqrt[3]{3}} = \frac{1}{2\sqrt[3]{3}}](/latexrender/pictures/378e05cf52f461fab9b27a29857c9105.png)

![\frac{1}{3\sqrt[3]{9}} \frac{1}{3\sqrt[3]{9}}](/latexrender/pictures/e8db584c1c98bc0938f8d512cad4e766.png)

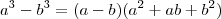



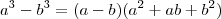
![\lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3} \lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}](/latexrender/pictures/0ebbfecbd124cb8629e1df0405735d32.png)
![\lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{(\sqrt[3]{x}-\sqrt[3]{3})(\sqrt[3]{x^2}+\sqrt[3]{3x}+\sqrt[3]{3^2})} \lim_{x\rightarrow3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{(\sqrt[3]{x}-\sqrt[3]{3})(\sqrt[3]{x^2}+\sqrt[3]{3x}+\sqrt[3]{3^2})}](/latexrender/pictures/ebae0af7bef623060e45d434681daabe.png)
![\lim_{x\rightarrow3}\frac{1}{(\sqrt[3]{x^2}+\sqrt[3]{3x}+\sqrt[3]{3^2})}= \frac{1}{3\sqrt[3]{9}} \lim_{x\rightarrow3}\frac{1}{(\sqrt[3]{x^2}+\sqrt[3]{3x}+\sqrt[3]{3^2})}= \frac{1}{3\sqrt[3]{9}}](/latexrender/pictures/84c467c15a8337364bb00f1b68487558.png)

