 por Lilica » Qua Jun 29, 2011 16:02
por Lilica » Qua Jun 29, 2011 16:02
Dê um exemplo de uma função f:R-R que é derivável em todos os pontos, exceto em x = 0 e x = 1.
Minha dúvida é a seguinte, encontrei uma função que não é derivável em 1 e 0, mas como posso provar que a mesma será derivável para todos os outros pontos?
-
Lilica
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Jun 29, 2011 15:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por LuizAquino » Qua Jun 29, 2011 16:32
por LuizAquino » Qua Jun 29, 2011 16:32
Qual foi a função que você encontrou?
A ideia nesses exercícios é começar com uma função que sabemos ser derivável em todos os seus pontos. Em seguida, manipulamos essa função de modo a ela ficar não diferenciável nos pontos desejados.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Lilica » Qua Jun 29, 2011 16:47
por Lilica » Qua Jun 29, 2011 16:47
Eu pensei nesta função:
f (x);
x+1 x<0
2x 0?x<1
x+2 se x?1
Conclui através das derivadas laterais que a mesma não é derivável em 1 nem em 0, mas não me garante que seja derivável em todos os outros pontos. Qual seria a sua idéia?
-
Lilica
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Jun 29, 2011 15:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por LuizAquino » Qua Jun 29, 2011 17:04
por LuizAquino » Qua Jun 29, 2011 17:04
Note que a sua função é formada por três pedaços, cada um sendo uma porção de reta. Ora, uma função do tipo

(a e b constantes reais) é derivável em todos os pontos de seu domínio! (Se você quiser, facilmente pode demonstrar isso.)
Por exemplo, a função h(x) = x + 1 é derivável em todos os pontos de seu domínio (que seria o conjunto dos números reais). É claro que
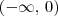
é um subconjunto do domínio de h, portanto ela é derivável nele. Em resumo, h é derivável para x < 0.
ObservaçãoPara provar que a sua função é diferenciável em todos os seus pontos, exceto em 0 e 1, você terá que provar que o limite

existe para três casos distintos:
(i) a < 0
(ii) 0 < a < 1
(iii) a > 1
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- A função é derivável
por Ana Maria da Silva » Qua Jun 12, 2013 20:51
- 1 Respostas
- 1180 Exibições
- Última mensagem por e8group

Sex Jun 14, 2013 20:41
Cálculo: Limites, Derivadas e Integrais
-
- Seja ?(x) uma função derivavel
por kak9 » Ter Out 02, 2018 15:33
- 0 Respostas
- 2976 Exibições
- Última mensagem por kak9

Ter Out 02, 2018 15:33
Cálculo: Limites, Derivadas e Integrais
-
- dúvida sobre função derivável
por MariPC » Sáb Ago 15, 2009 14:45
- 6 Respostas
- 6322 Exibições
- Última mensagem por MarceloFantini

Sex Jun 03, 2011 16:02
Cálculo: Limites, Derivadas e Integrais
-
- Análise de derivável
por Claudin » Dom Set 25, 2011 17:35
- 3 Respostas
- 1239 Exibições
- Última mensagem por LuizAquino

Sáb Out 01, 2011 09:45
Cálculo: Limites, Derivadas e Integrais
-
- ponto da reta r que é eqüidistante do ponto A e do ponto B
por gutorocher » Qua Jul 21, 2010 14:01
- 12 Respostas
- 15159 Exibições
- Última mensagem por gutorocher

Sex Jul 23, 2010 13:04
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 (a e b constantes reais) é derivável em todos os pontos de seu domínio! (Se você quiser, facilmente pode demonstrar isso.)
(a e b constantes reais) é derivável em todos os pontos de seu domínio! (Se você quiser, facilmente pode demonstrar isso.)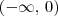 é um subconjunto do domínio de h, portanto ela é derivável nele. Em resumo, h é derivável para x < 0.
é um subconjunto do domínio de h, portanto ela é derivável nele. Em resumo, h é derivável para x < 0. existe para três casos distintos:
existe para três casos distintos: .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
