 por sofa » Qua Jun 29, 2011 04:42
por sofa » Qua Jun 29, 2011 04:42
Não estou conseguindo sair da indeterminação
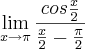
transformando aquele cosseno em um seno e invertendo ele eu cheguei ate
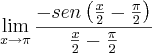
(fiquei na duvida se poderia inverter o seno)
se estivesse tendendo a zero eu diria que o resultado é -1 (e é realmente -1) mas como esta tendendo a pi eu fquei na duvida sobre o que fazer
resultado pelo wolfram
http://www.wolframalpha.com/input/?i=li ... -pi%2F2%29mas preciso saber sem ser por l'Hôpital.
-
sofa
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jun 29, 2011 04:18
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Jun 29, 2011 04:59
por MarceloFantini » Qua Jun 29, 2011 04:59
Como vocÊ transformou o cosseno em seno?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por sofa » Qua Jun 29, 2011 05:07
por sofa » Qua Jun 29, 2011 05:07
Sim, transformei, ficou do jeito ali da segunda equação
o seno ali ta negativo mas eu acho que ta errado isso que eu fiz, o certo é
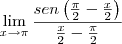
mas mesmo assim não consigo sair disso, n sei se estou indo pelo caminho certo
-
sofa
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jun 29, 2011 04:18
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Jun 29, 2011 05:19
por MarceloFantini » Qua Jun 29, 2011 05:19
Agora entendi. O que você fez está certo: primeiro, usou que cosseno é apenas seno deslocado de

, e portanto

. Agora só faltou lembrar que

, e portanto
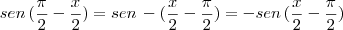
. Com isso, você cai no limite fundamental do seno e termina a questão.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por sofa » Qua Jun 29, 2011 05:29
por sofa » Qua Jun 29, 2011 05:29
mas para cair no limite fundamental do seno x deveria estar tendendo a 0 e neste caso esta tendendo a pi
-
sofa
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jun 29, 2011 04:18
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Jun 29, 2011 06:08
por MarceloFantini » Qua Jun 29, 2011 06:08
Essa é uma confusão que acontece constantemente. Não é a variável que tem que tender a zero. Note que se você fizer o limite com x tendendo a zero NÃO sairá o limite fundamental. O importante a saber é: o que tem que estar tendendo a zero é o
denominador e o que estiver
dentro do seno. Se tivessemos um limite assim:
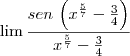
Para que isto seja um limite fundamental, não devemos ter

mas sim
![x \to \sqrt[5]{\left(\frac{3}{4}\right)^7} x \to \sqrt[5]{\left(\frac{3}{4}\right)^7}](/latexrender/pictures/f7c4ad855979d0447d1149824d7d088d.png)
pois é ele quem zera quem está
dentro do seno e quem está no
denominador.
Espero que isso tenha esclarecido a sua dúvida e resolvido sobre porque está certo.

Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por sofa » Qua Jun 29, 2011 06:25
por sofa » Qua Jun 29, 2011 06:25
Entendi agora, estava no caminho certo então, só faltava esclarecer isso
Obrigado Marcelo
-
sofa
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jun 29, 2011 04:18
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] função trigonométrica
por rafaelbr91 » Ter Mar 27, 2012 17:51
- 2 Respostas
- 2171 Exibições
- Última mensagem por rafaelbr91

Ter Mar 27, 2012 18:43
Cálculo: Limites, Derivadas e Integrais
-
- Limite de uma função trigonométrica
por Douglas16 » Seg Mar 11, 2013 14:45
- 1 Respostas
- 1392 Exibições
- Última mensagem por Douglas16

Seg Mar 11, 2013 15:32
Cálculo: Limites, Derivadas e Integrais
-
- Limite de uma função trigonométrica
por Douglas16 » Sáb Mar 16, 2013 21:52
- 3 Respostas
- 2226 Exibições
- Última mensagem por e8group

Dom Mar 17, 2013 00:34
Cálculo: Limites, Derivadas e Integrais
-
- Limite de função trigonométrica
por Carolminera » Qui Jul 17, 2014 15:44
- 4 Respostas
- 2999 Exibições
- Última mensagem por Carolminera

Dom Jul 20, 2014 21:52
Cálculo: Limites, Derivadas e Integrais
-
- Limite de função trigonométrica
por Fernandobertolaccini » Qua Jul 30, 2014 23:27
- 1 Respostas
- 2697 Exibições
- Última mensagem por Man Utd

Qui Ago 07, 2014 15:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
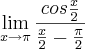
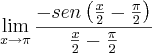




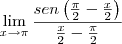
 , e portanto
, e portanto  . Agora só faltou lembrar que
. Agora só faltou lembrar que  , e portanto
, e portanto 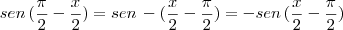 . Com isso, você cai no limite fundamental do seno e termina a questão.
. Com isso, você cai no limite fundamental do seno e termina a questão.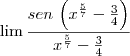
 mas sim
mas sim ![x \to \sqrt[5]{\left(\frac{3}{4}\right)^7} x \to \sqrt[5]{\left(\frac{3}{4}\right)^7}](/latexrender/pictures/f7c4ad855979d0447d1149824d7d088d.png) pois é ele quem zera quem está
pois é ele quem zera quem está 

 .
.



