 por benni » Ter Jun 28, 2011 15:21
por benni » Ter Jun 28, 2011 15:21
Seja a função h(x)=

a) determine o subconjunto de R tal que:
a1) h(x) > 0
a2) h(x) < 0
a3) h(x) = 0
-
benni
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Mar 02, 2011 15:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por meuemail » Ter Jun 28, 2011 18:16
por meuemail » Ter Jun 28, 2011 18:16
Não enviar apenas enunciado.
-
meuemail
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Dez 11, 2010 23:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por benni » Ter Jun 28, 2011 21:06
por benni » Ter Jun 28, 2011 21:06
a) { x

R | 0< x< Pí}
b) { x

R |- pí <x<0}
c) Vazio
Estou na duvida.
-
benni
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Mar 02, 2011 15:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por MarceloFantini » Ter Jun 28, 2011 22:23
por MarceloFantini » Ter Jun 28, 2011 22:23
Se a função seno estiver definida de
![[-\pi, \pi] [-\pi, \pi]](/latexrender/pictures/86f9a3a2cc344b78b146c202b2226bae.png)
, está certo. Digo isso porque não custa nada colocar o
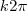
para indicar todos os valores possíveis. De resto as respostas estão certas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por arima » Seg Jul 04, 2011 19:36
por arima » Seg Jul 04, 2011 19:36
Neste exercíco pede o dominio da função e estou com duvida?
Calcule o Dom(h).
Gostaria que alguem verificasse se a minha resposta esta certa.
Para que exista sin(x)?0 os valores de x que sen(x)=0 é x=0 x=? x=k?
Portanto seu domínio será Dom(h)={x?R/ x?0 ,x?k? e x>0}
Obrigada.
-
arima
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sáb Out 23, 2010 18:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por MarceloFantini » Seg Jul 04, 2011 20:00
por MarceloFantini » Seg Jul 04, 2011 20:00
Arima, sua resposta não faz sentido. Por favor releia a minha resposta mais atentamente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por cicero » Sáb Jul 09, 2011 19:49
por cicero » Sáb Jul 09, 2011 19:49
É PREOCUPANTE PERCEBE QUE "PROFESSORES DE MATEMÁTICA" QUE ESTÃO FAZENDO UM CURSO DE PÓS-GRADUAÇÃO, NAO SAIBAM RESOVLER PROBLEMAS SIMPLES COMO ESTES.
FICA AQUI UMA CRITICA A TODOS , QUE DEDICAM O SEU TEMPO EM BUSCAR AS RESPOSTAS PRONTAS EM SITES DE AJUDA, ALIÁS, NEM SE QUER TENTAM RESOLVER OS PROBLEMAS, POSTAM E PEDEM PARA QUE ALGUEM OS RESOLVAM PARA SI. DEPOIS QUEREMOS COBRAR DE NOSSOS ALIUNOS DEDICAÇÃO E SERIEDADE EM SEUS ESTUDOS. POR FAVOR, NÃO SEJAM DEMAGOGOS E HIPÓCRITAS.
E AINDA SE DIZEM SEM TEMPO PARA ESTUDAR E PEDIR AS PESSOAS CERTAS QUE TIREM SUAS DÚVIDAS.
TUTOR ON-LINE.
-
cicero
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Dom Jun 26, 2011 16:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Educação Matemática/Modelagem Matemática
- Andamento: formado
 por cicero » Sáb Jul 09, 2011 19:54
por cicero » Sáb Jul 09, 2011 19:54
A FUNÃO SENO É UMA FUNÇÃO DEFINIDA EM TODA RETA, PARA VOCÊS QUE NÃO SABEM, QUANDO DIGO TODA RETA ME REFIRO AO CONJUNTOD OS NÚMEROS REAIS. E O QUE ESTÁ ESCRITO NESSA RESPOSTA ESTÁ TOTALMENTE INQUERENTE. TOME CUIDADO AO SOMENTE COPIAR UMA RESPOSTA, SEM AO MENSO TER A CAPACIDADE DE ANALISÁ-LA E VERIFICAR SE ESTA ESTÁ CORRETA.
-
cicero
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Dom Jun 26, 2011 16:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Educação Matemática/Modelagem Matemática
- Andamento: formado
 por benni » Qua Jul 27, 2011 15:39
por benni » Qua Jul 27, 2011 15:39
Em parte tu tens toda razão e ao mesmo tempo"Não" ,pois quando estou em sala sinto que meus alunos não tem a base suficiente e dai a necessidade de adequar a esta realidade, a qual é provocada pelo sistema. Este mesmo sistema forma professores com esta qualidade e apenas alguns afortunados podem frequentar universidades de qualidade.Portanto .Será culpa dos professores ? Muitos estão sem reciclagem a anos e muitos estão tentando se reciclar . Não é fácil, mas também não é desculpa, apenas entenda a realidade de cada um. Pelo jeito " Ema Ema Ema cada um com seus PROBREMA" .
-
benni
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Mar 02, 2011 15:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5572 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4589 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5745 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3484 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2952 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 R | 0< x< Pí}
R | 0< x< Pí} R |- pí <x<0}
R |- pí <x<0}
![[-\pi, \pi] [-\pi, \pi]](/latexrender/pictures/86f9a3a2cc344b78b146c202b2226bae.png) , está certo. Digo isso porque não custa nada colocar o
, está certo. Digo isso porque não custa nada colocar o 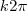 para indicar todos os valores possíveis. De resto as respostas estão certas.
para indicar todos os valores possíveis. De resto as respostas estão certas.









 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.