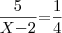 COM
COM  ?
?gente como que faz uma equação com 4 inconigita?
"3bx + 6bc = 7bx + 3bc?"
só sei com duas.

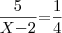 COM
COM  ?
?
zekinha escreveu:ALGUEM SABE TIRA O MINIMO DESSA EQUAÇÃO?COM
?
gente como que faz uma equação com 4 inconigita?
"?"
só sei com duas.
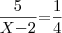 COM
COM  ?
?



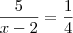

Claudin escreveu:
E sobre as incógnitas
Agora basta substituir os respectivos valores.




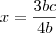
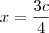

zekinha escreveu:Não entendi muito bem =(
essa do 3bx + 6bc = 7bx + 3bc

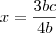
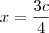 ?
? 


 é de
é de  .
.
zekinha escreveu:Exemplo:
12x – 14(1 - x) -2 (10x + 4) = 0 ? aplicar a propriedade distributiva
12x - 14 +14x - 20x - 8 = 0 ... Porque? Que é " +14x " ? Sendo que o sinal no item vermelhoé de
.
O mesmo ocorre neste aqui
4x – 6 (4 – x) = 10 + 8 (2x + 1) ? aplicar a propriedade distributiva
4x – 24 +6x = 10 + 16x + 8 Não entendo, o sinal não era para ser -6x ?


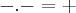
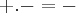

 e logo em seguida
e logo em seguida 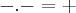

zekinha escreveu:Exemplo:
12x – 14(1 - x) -2 (10x + 4) = 0 ? aplicar a propriedade distributiva
12x - 14 +14x - 20x - 8 = 0 ... Porque? Que é " +14x " ? Sendo que o sinal no item vermelhoé de
.
O mesmo ocorre neste aqui
4x – 6 (4 – x) = 10 + 8 (2x + 1) ? aplicar a propriedade distributiva
4x – 24 +6x = 10 + 16x + 8 Não entendo, o sinal não era para ser -6x ?


 normal e com o
normal e com o 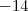 eu vou fazer a distributiva, blza até aqui. Agora, eu vou multiplicar 1º o 1 certo?
eu vou fazer a distributiva, blza até aqui. Agora, eu vou multiplicar 1º o 1 certo? 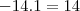 Dai multiplica o 2º que é o
Dai multiplica o 2º que é o 


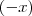 ficara
ficara 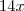 ou
ou 
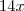 mas, não faz sentido sendo que o que multiplica o (1 - x) que no caso é o -14x é negativo
mas, não faz sentido sendo que o que multiplica o (1 - x) que no caso é o -14x é negativo ser
ser  ser
ser 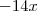 e não
e não 

zekinha escreveu:Ai fica assim: Copia onormal e com o
eu vou fazer a distributiva, blza até aqui. Agora, eu vou multiplicar 1º o 1 certo?
zekinha escreveu:fica
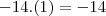
zekinha escreveu:Dai multiplica o 2º que é o
 e não apenas
e não apenas 
zekinha escreveu:

ficara
ou

zekinha escreveu:Na resolução estámas, não faz sentido sendo que o que multiplica o (1 - x) que no caso é o -14x é negativo
era pra oser
ser
e não





Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
