


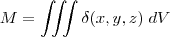

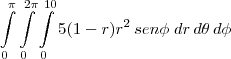


 a densidade de massa no ponto
a densidade de massa no ponto 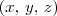 .
. ;
;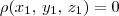 , com
, com 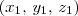 um ponto sobre a esfera;
um ponto sobre a esfera; decai proporcionalmente à distância do centro.
decai proporcionalmente à distância do centro.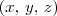 ao centro da esfera. Podemos reescrever (i), (ii) e (iii) como:
ao centro da esfera. Podemos reescrever (i), (ii) e (iii) como: ;
; ;
;  , com k e m constantes reais.
, com k e m constantes reais. .
. .
.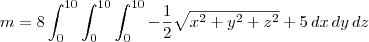


 mas a resposta é a mesma do Luiz Aquino. O número 8 está ali apenas para deixar os limites de integração mais bonitinhos, haha.
mas a resposta é a mesma do Luiz Aquino. O número 8 está ali apenas para deixar os limites de integração mais bonitinhos, haha.

MarceloFantini escreveu:Bom, esqueci domas a resposta é a mesma do Luiz Aquino.
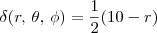 ao invés de
ao invés de  .
.MarceloFantini escreveu:O número 8 está ali apenas para deixar os limites de integração mais bonitinhos, haha.




Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)